Les * signifient que la correction est disponible.

Exercice *f1/ ☆ L'exercice consiste à définir la fonction dicho qui a pour paramètres deux nombres a et b, une fonction f continue monotone sur [a,b] telle que f(a)*f(b) <0, et une précision e. Cette fonction doit renvoyer une approximation du zéro* de f ,appartenant à [a,b], avec une précision inférieure à e et par dichotomie. Correction
* c'est-à-dire l'abscisse x telle que f(x)=0.

EXPLICATION dichotomie : [Afficher]

L'idée de la dichotomie est d'aller évaluer f au milieu du segment [a,b], c'est-à-dire en d=(a+b)/2 : si f(a)*f(d) est négatif alors c se situe dans [a,d], sinon il se situe dans [d,b].
Tant que l'intervalle trouvé n'est pas de longueur inférieure à la précision e, on continue à diminuer l'intervalle en regardant le signe du produit des images des bornes de l'intervalle.
Voici un exemple de début de dichotomie :

EXPLICATION existence d'un zéro : [Afficher]

f étant continue monotone sur [a,b] telle que f(a)*f(b)<0, d'après le théorème des valeurs intermédiaires il existe un unique c compris entre a et b tel que f(c)=0. Donc ce que l'on cherche avec la fonction dicho existe bien (car il s'agit de c) !

Exercice *f2/ ★☆ L'exercice consiste à créer une fonction récursive facto qui a pour paramètre un entier naturel n et qui renvoie n! , c'est-à-dire n(n-1)(n-2)...3x2x1 . Correction

DÉFINITION Récursif :[Afficher]

"Se dit d'un programme informatique organisé de manière telle qu'il puisse se rappeler lui-même, c'est-à-dire demander sa propre exécution au cours de son déroulement." d'après Larousse.

Exercice *f3/ ★ L'exercice consiste à créer une fonction Euclide qui a pour paramètres deux entiers naturels non nuls a et b, et qui renvoie (en utilisant la méthode d'Euclide) le plus grand diviseur commun à a et à b. Correction

EXPLICATION Théorème : [Afficher]

Soient a et b deux entiers naturels avec b non nul. Alors il existe un unique entier naturel q et un unique entier naturel non nul r tels que a=b.q+r avec r compris entre 0 (inclus) et |b| (exclu).

EXPLICATION Algorithme d'Euclide : [Afficher]

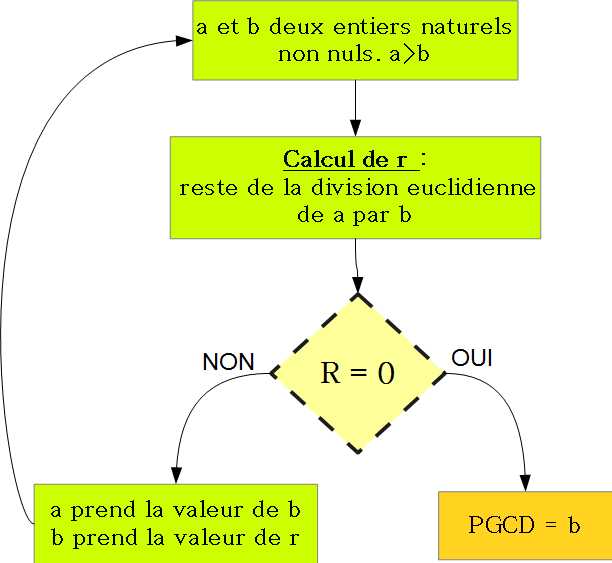
On a deux entiers naturels non nuls a et b tel que a>b.

- A partir du théorème précédent on calcule le reste de la division euclidienne de a par b.
- Si ce reste est nul alors b correspond au plus grand diviseur commun (PGCD) à a et à b car on obtient une équation de la forme a=bq.
- Sinon, il faut recommencer le calcul en donnant la valeur de b à a et la valeur de r à b jusqu'à obtenir un reste nul.

Exercice *f4/ ★ Cet exercice consiste à créer une fonction convertDB qui a pour paramètre un entier naturel dec et qui renvoie la conversion de ce nombre en binaire.Correction

EXPLICATION conversion décimal -> binaire : [Afficher]

Pour un nombre décimal entier naturel, il faut faire la division euclidienne du nombre décimal par 2, puis recommencer avec le nouveau nombre.... jusqu'à obtenir un quotient de 0.
Le nombre binaire obtenu sera la juxtaposition des restes (le premier reste calculé sera le chiffre le plus à droite en binaire).
Par exemple, voici les calculs pour obtenir la conversion de l'entier 32 en nombre binaire :
convertDB

Exercice *f5/ ★☆ Cet exercice consiste à créer une fonction convertBD qui a pour paramètre un nombre binaire b et qui renvoie la conversion de ce nombre en décimal. Correction

EXPLICATION conversion binaire --> décimal : [Afficher]

Voici un petit exemple :
convertBDex

AIDE possible : [Afficher]

Convertir le nombre binaire en chaine de caractères pour pouvoir parcourir ce nombre chiffre par chiffre plus facilement.

Exercice *f6/ ☆ Créez une fonction qui demande un nombre à l'utilisateur et affiche si ce nombre est pair ou impair. Correction

Exercice *f7/★☆ Soit x(t), qui pour a pour dérivée f(x(t)).
Créez une fonction Euler qui a pour paramètres une fonction f, un intervalle de temps dt, un temps maximal tmax et la valeur initiale de x, et qui renvoie la liste des valeurs de x(t) à l'aide de la méthode d'Euler. Correction

OUTILS méthode d'Euler : [Afficher]

Voici ce qui vous est utile dans cet exercice. Attention, cet outil a été simplifié dans le cadre de cet exercice. Dans le cas où :
Euler

Pour plus d'explication : http://www.tangentex.com/MethodeEuler.htm

Exercice *f8/ - Créez une fonction maximum qui prend en paramètres 3 nombres et qui renvoie le plus grand d'entre eux. Correction

Exemple : maximum(0.1,5.2,6) doit nous renvoyer 6.