Les * signifient que la correction est disponible.

Exercice S1/ ★☆ La suite de Syracuse est définie par :

pour plus d'information sur cette suite: http://www.les-suites.fr/suite-de-syracuse.htm
                                 a. Créez une fonction nommée Syracuse qui a pour paramètres le premier terme de la suite, noté U0, et un entier naturel n. Cette fonction doit renvoyer la valeur de Un. (pour U0=15 on a U7=160)
La conjecture de Syracuse dit que la suite de Syracuse atteint 1. On appelle temps de vol le plus petit indice n tel que Un=1.
                                 b. Créez une fonction nommée tempvol qui a pour paramètre le premier terme de la suite, noté U0, et qui renvoie le temps de vol. (tempvol(15)=17)
Le temps de vol en altitude est le plus grand indice n tel que Un+1 est inférieur ou égal à U0.
                                 c. Créez une fonction nommée altivol qui a pour paramètre le premier terme de la suite, noté U0, et qui renvoie le temps de vol en altitude. (altivol(15)=10)
L'altitude maximale est la valeur maximale de la suite.
                                 d. Créez une fonction nommée altimax qui a qui a pour paramètre le premier terme de la suite, noté U0, et qui renvoie l'altitude maximale. ( altimax(15)=160 )   La correction arrivera un autre jour...

Exercice *S2/ ★ La suite de Fibonacci est définie par :

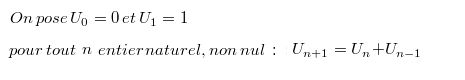
L'exercice consiste à créer une fonction non récursive (i.e. itérative) Fibo qui a pour paramètre un entier naturel n non nul et qui renvoie Un.
Correction

Voici quelques valeurs pour vérifier votre fonction :

U0	U1	U2	U3	U4	U5	U6	U7	U8	U9	U10
0	1	1	2	3	5	8	13	21	34	55

DÉFINITION Récursif : [Afficher]

"Se dit d'un programme informatique organisé de manière telle qu'il puisse se rappeler lui-même, c'est-à-dire demander sa propre exécution au cours de son déroulement." d'après Larousse.
La correction arrivera un autre jour...pour plus d'information sur cette suite: https://fr.wikipedia.org/wiki/Suite_de_Fibonacci

CONTEXTUALISATION Fibonacci : [Afficher]

On considère une espèce F. Chaque couple de cette espèce engendre à chaque début de mois un nouveau couple à compter du début du 3ème mois de son existence. Sachant qu'aucun individu ne meurt et qu'à l'instant initial considéré il n'existe qu'un couple de cette espèce, Combien de couple obtient-on au début du n-ième mois ?
Réponse: [Afficher]

On pose

le nombre de couples de l'espèce F au début du mois n.
Au début du mois n, les couples existants sont ceux engendrés par la population datant du début du mois n-2 et ceux existants déjà au début du mois n-1. Donc on a : fibo

Exercice *S3/ ★☆ Reprenez la définition de la suite de Fibonacci donnée dans l'exercice précédent. L'exercice consiste à créer une fonction récursive FiboR qui a pour paramètre un entier naturel n et qui renvoie Un. Correction

Exercice S4/ ★★ Reprenez la définition de la suite de Fibonacci donnée dans l'exercice précédent. L'exercice consiste à créer une fonction récursive terminale FiboRT qui a pour paramètres un entier naturel n non nul, et les conditions initiales U0 et U1, et qui renvoie Un.

DÉFINITION Récursif terminal : [Afficher]

"Une définition de fonction f est récursive terminale quand tout appel récursif est de la forme return f(...); ; autrement dit, la valeur retournée est directement la valeur obtenue par un appel récursif, sans qu'il n'y ait aucune opération sur cette valeur." d'après http://cermics.enpc.fr/polys/info1/main/node22.html

Exercice *S5/ ★★ Le nombre d'or est la limite de la suite notée Vn et définie à partir de la suite Un de Fibonacci. Voici comment on les définit :
nbror

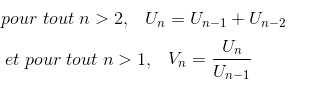
On prend V1=0, U1=1 et U2=2.
L'exercice consiste à créer une fonction nbr_or qui a pour paramètre un nombre e strictement inférieur à 1, et qui renvoie une approximation de la valeur du nombre d'or avec une précision e.
Correction

PS: Si vous voulez faire un peu de maths, vous pouvez prouver que la limite de Vn est le nombre d'or (cf DÉMONSTRATION lien entre nombre d'or et suite de Fibonacci).

DÉFINITION: Nombre d'or :[Afficher]

nombre d'or est définit comme étant l'unique valeur positive asurb

telle que

avec a > b.
i.e, << a est à b ce que a+b est à a>>.

DÉMONSTRATION Lien entre nombre d'or et suite de Fibonacci : [Afficher]

On va expliciter l'expression de la suite de Fibonacci, puis trouver un équivalent du rapport entre deux termes consécutifs. Cet équivalent est la limite, et doit donc être le nombre d'or.

Exercice *S6/ ☆ On définit la suite Un de la façon suivante :

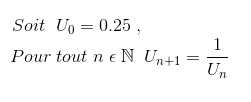
1) L'exercice consiste à créer une fonction U qui a pour paramètre un entier naturel n non nul et qui renvoie la liste des itérations de Un : [U0, U1,..,Un,Un+1]
2) A partir de cette fonction, afficher un graphique représentant les 12 premiers termes de la suite Un en fonction de leur indice.
Correction

Exercice *S7/ ★★ On définit la suite Un de la façon suivante :
suite_de_fonction

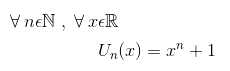
Tracer Un(x) pour les différents entiers naturels n appartenant à l'intervalle [1 , 5], et pour tout x appartenant à l'intervalle [0 , 10].
Correction

AIDE : [Afficher]

                     Étape 1 : Créer une fonction U qui a pour paramètres un entier naturel n et une liste de valeurs réelles X et qui renvoie la liste des images des éléments de X par Un.
                     Étape 2 : Créer une liste X de x appartenant à l'intervalle [0 , 10]
                     Étape 3 : Appliquer U à X pour différent n entier naturel appartenant à l'intervalle [1 , 5], et afficher le résultat à chaque fois.