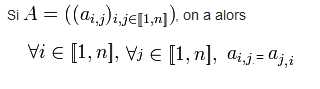Les * signifient que la correction est disponible

Exercice *M1/ ★ L'exercice consiste à créer une fonction diagdom qui a pour paramètre une matrice A carrée et qui renvoie True si la matrice est à diagonale dominante, ou False dans le cas contraire. (ici False et True sont des booléens, pas une chaîne de caractères) Correction

DÉFINITION diagonale dominante : [Afficher]

Soit A une matrice carrée à diagonale dominante,

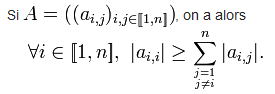
pour plus d'explication : https://fr.wikipedia.org/wiki/Matrice_%C3%A0_diagonale_dominante

     EXEMPLE de matrice à diagonale dominante : [Afficher]

Exercice *M2/ ★ L'exercice consiste à créer une fonction exp non récursive qui a pour paramètres une matrice A carrée et un entier k et qui renvoie l'exponentielle de A à l'ordre k. Correction

DÉFINITION exponentielle d'une matrice : [Afficher]

Soit A une matrice, on a :

pour plus d'explication : https://fr.wikipedia.org/wiki/Exponentielle_d'une_matrice

Or nous voulons l'exponentielle de A à l'ordre k. Pour cela nous arrêtons la somme à n=k.

Exercice M3/ ★☆ L'exercice consiste à créer une fonction expR récursive qui a pour paramètres une matrice A et un entier k et qui renvoie l'exponentielle de A à l'ordre k. (cf définition à l'exercice M2)

DÉFINITION Récursif: [Afficher]

"Se dit d'un programme informatique organisé de manière telle qu'il puisse se rappeler lui-même, c'est-à-dire demander sa propre exécution au cours de son déroulement." d'après Larousse.

Exercice *M4/ ☆ L'exercice consiste à créer une fonction mult qui a pour paramètres deux matrices A et B et qui renvoie le produit matriciel AB (sans utiliser la fonction dot(A,B) qui renvoie déjà AB). Correction

EXPLICATION Multiplication Matricielle: [Afficher]

Soit p, le nombre de colonne de A, et le nombre de ligne de B.
Soit C la matrice égale au produit de A par B. L'élément i,j de C est définit par la somme suivante :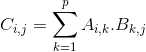 mult1

Exercice M5/ ★ L'exercice consiste à créer une fonction sym qui a pour paramètre une matrice carrée A et qui renvoie True si la matrice est symétrique et False sinon.

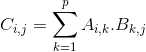
DÉFINITION symétrique :[Afficher]

Soit A une matrice symétrique,

Exercice *M6/ - L'exercice consiste à créer une fonction pdtvecto qui a pour paramètres deux vecteurs X et Y à 3 coordonnées, et qui renvoie le produit vectoriel de X avec Y. Correction

EXPLICATION Produit vectoriel :[Afficher]

Soit u et v deux vecteurs à 3 coordonnées. Le produit vectoriel de X par Y est définit de la manière suivante :

Exercice *M7/ - Un chevalier et un martien vont au supermarché trois fois dans la semaine. Leurs nourrices voudraient savoir s’ils font attention aux prix.
A l’aide de la fonction np.linalg.solve, retrouve le prix de ce qu’ils ont acheté en connaissance de ce tableau : Correction

	Sabres achetés	Paquets de chips achetés	Paquets de craies achetés	dépenses totale
1ère fois	1	3	2	15 €
2ième fois	2	1	1	19 €
3ième fois	5	2	3	48 €

Aide :[Afficher]

On passe d’un système de 3 équations à 3 inconnues à une équation matricielle, de la façon suivante :

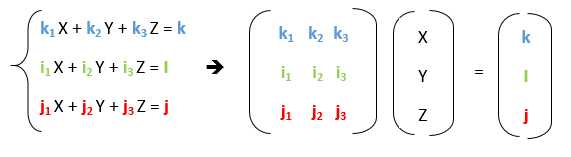
Exercice *M8/ ☆ Le tableau ci-dessous donne la hauteur de pins blancs en fonction de leurs diamètres. Réécrivez ce tableau dans un objet numpy.array et affichez :
-    La hauteur moyenne,
-    Le diamètre moyen,
-    Le diamètre de l’arbre le plus grand. Correction

Hauteur	127	119	135	132	130	130	110	75	110	124
Diamètre	21.2	20.2	24.6	23	27.2	18.6	17.3	10	19.7	22.3