♣ Exercice G1 :
A l'aide de la fonction Axes3D.plot( ), tracez les points suivant en les reliant dans l'ordre :

	X	Y	Z
A	0	0	0
B	1	1	0
C	1	1	1
D	0	0	1

Il faut également relier les points D et A.

Voici ce que l'on doit obtenir (figure 1) :

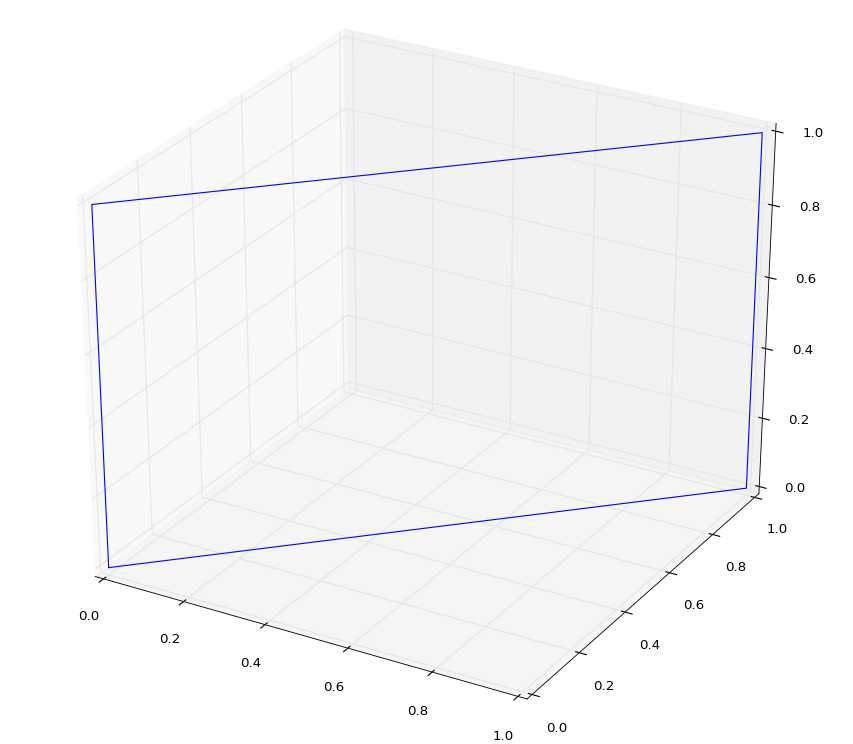
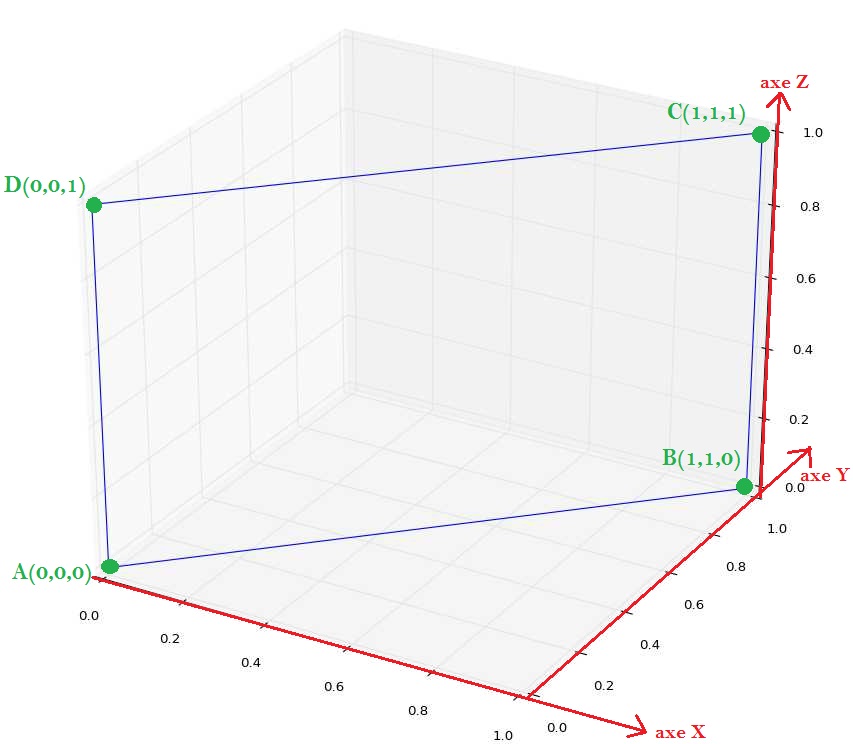
Voici une solution testée sous python 3.4 :

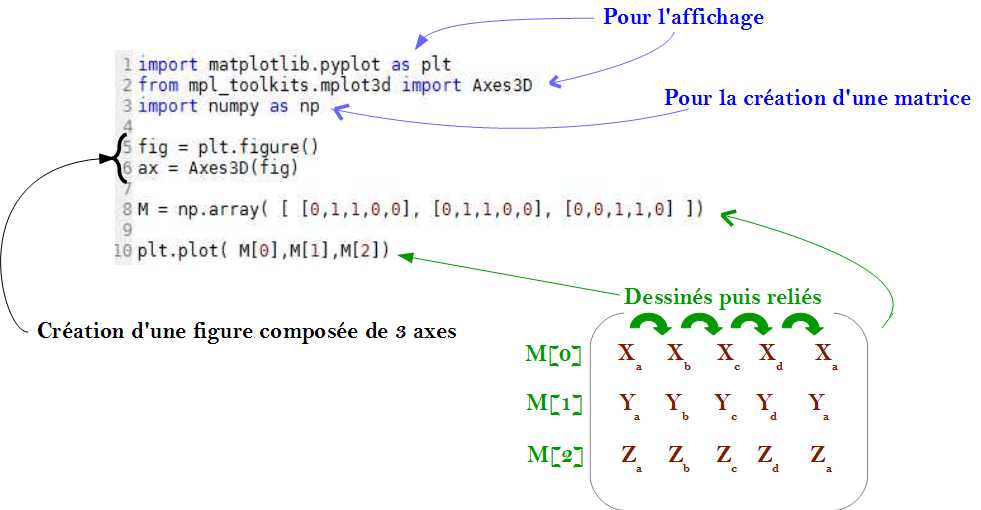
♣ Exercice G2 :
Dessinez un cube sur un graphique 3D.

Voici la figure que l'on doit obtenir et une solution testée sous python 3.4 :

dessiner_un_cube_illustration

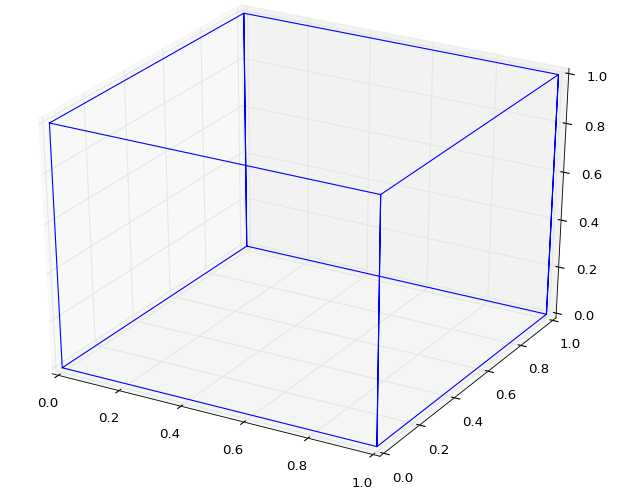
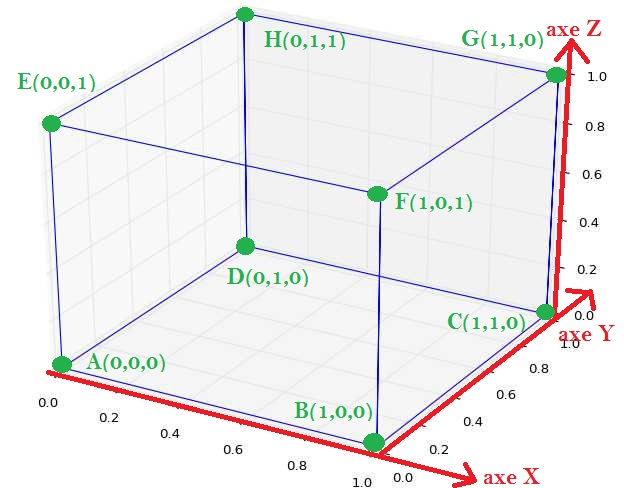
Pour relier les sommets A,B,C,D,E,F,G et H d'un cube on peut parcourir le cube ainsi : A → B → C → D → A (carré bas tracé) → E → F → B → F → G → C → G → H → D → H → E (carré haut tracé et relié au carré bas)
On peut donc créer la matrice de coordonnées M dont la première ligne correspond à la liste des abscisses des points parcourus, tandis que la deuxième est la liste des ordonnées des points parcourus, et la troisième est la liste des côtes des points parcourus.

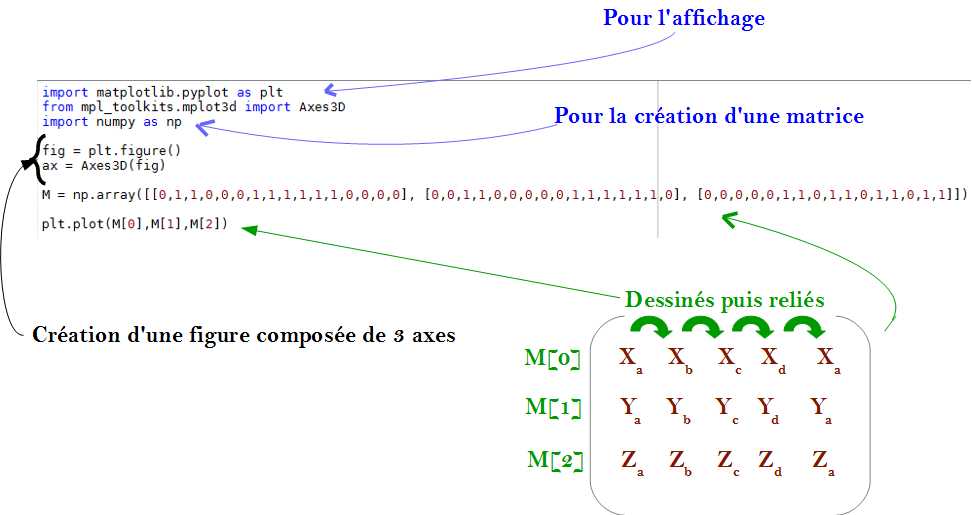
♣ Exercice G3 :
Une bille est poussée sur un circuit. Un logiciel repère sa position (X,Y) à chaque instant t = 0.05s environ et la référence dans le tableau suivant : cf. énoncé.
Simulez le parcours de la bille à l'aide de matplotlib.

Voici une solution implémentée en python 3.4 :
Code copiable :[Afficher]

import matplotlib.pylab as plt

X = [1,1.25,1.75,2.5,3.5,6,7.25,8,8.4,7.6,6.9,6.26,5.35]
Y = [15,13,10.5,7,3,0,2,4.25,5.5,3,1.2,0.09,0.16]

n = len(X)
plt.xlim(-0.2,9)
plt.ylim(-0.2,16)

for i in range(n):
plt.plot(X[i],Y[i],'o')
plt.pause(0.05)

L1. Importation avec alias de matplotlib.pylab.

L3 à L4. Création de X (resp. Y), la liste des distances (resp. la liste des hauteurs).

L6. Création de n à partir du nombre de distances référencées, n étant le nombre de positions référencées.

L7 à L8. Fixation des valeurs limites des axes pour un affichage plus propre.

Boucle FOR : L11. Pour chaque point référencé,
L12. On affiche le point,
L13. Et on fait une pause de 0.05s pour être en accord avec le tableau.
Fin Boucle FOR

Voici la fenêtre obtenue après un peu d'attente (les points s'affichent un par un) :

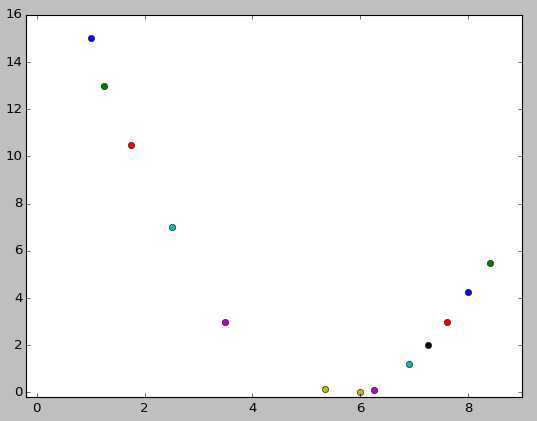
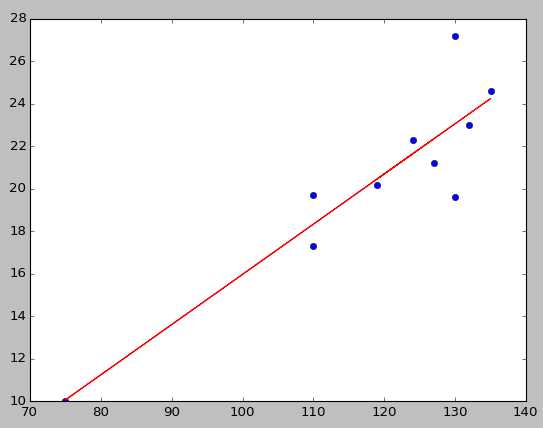
♣ Exercice G4 : Le tableau de l'énoncé donne la hauteur de pins blancs en fonction de leurs diamètres. L'exercice consiste à afficher une droite approximant au mieux la hauteur en fonction du diamètre (Une régression linéaire). On peut trouver les coefficients de la droite grâce à scipy.stats.linregress.

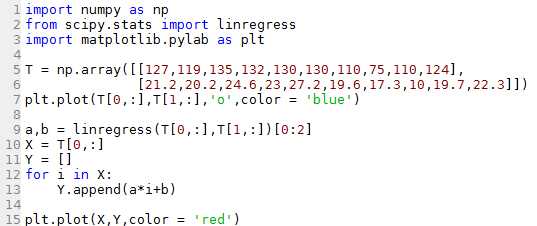G4py34

L1. à L3. On importe numpy pour travailler avec des tableaux (array), linregress pour faire la régression linéaire demandée, et matplotlib.pylab pour l'affichage graphique.

L5. à L6. On crée notre tableau avec : pour la première ligne les hauteurs des pins blancs et pour la seconde ligne les diamètres.
L7. On affiche tous les points (hauteur,diamètre) sur un graphique.

L9. On fait notre régression linéaire sur les lignes du tableau et on récupère les coefficients a et b caractérisant la droite voulue, d'équation y = ax+b.
L10. On crée notre liste X d'abscisses. Elle servira à l'affichage de la droite.
L11. On crée notre liste Y des ordonnées. Elle servira à l'affichage de la droite.
Boucle for : L12. On remplit la liste Y, pour chaque élément de X :
L13. On met l'élément a*i+b dans Y.
Fin boucle for

L15. On affiche la droite en se servant des valeurs de X et de Y.

♣ Exercice G5 : Affichez les valeurs de la fonction f(x) = x^2 + 6x +2 pour x allant de 0 à 10 avec un pas de 0.5.

Voici une solution implémentée en python 3.4 :

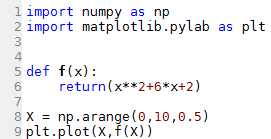
L1. On importe numpy pour la création de la liste des abscisses.
L2. On importe matplotlib.pylab pour l'affichage graphique.

L5. à L6. On définit la fonction f qui à une valeur x associe x^2 + 6x +2.

L8. On crée la liste des abscisses (allant de 0 à 10 avec un pas de 0.5).
L9. On affiche f(X) en fonction de X à l'aide de la fonction plot.
f(X) nous renvoie bien la liste des valeurs de f pour chaque élément de la liste X.

Voici le graphique obtenu :

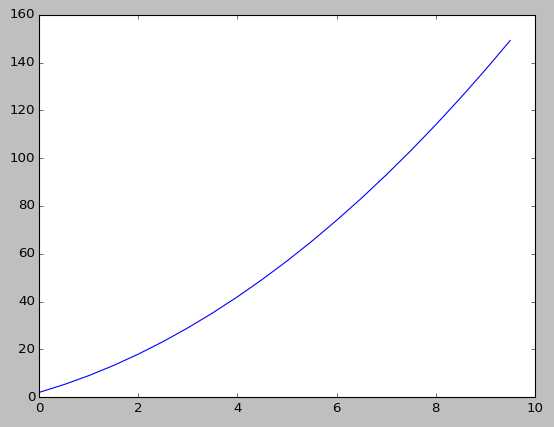
Remarque : La fonction f est ici une fonction très simple qui peut également être définie grâce à la fonction lambda. Le script devient alors le suivant : [Afficher]

import numpy as np
import matplotlib.pyplot as plt

f = lambda x : x**2 + 6*x + 2

X = np.arange(0,10,0.5)
plt.plot(X,f(X))

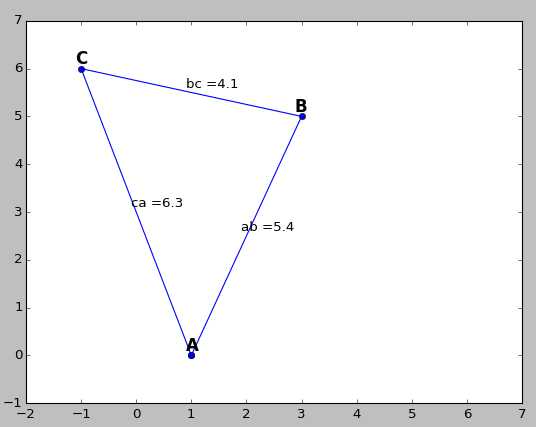
♣ Exercice G6 : Créez une fonction qui prend en paramètres 3 points (array colonne) a, b et c et qui affiche le triangle correspondant avec les noms des points et les longueurs des côtés du triangle.

Code copiable : [Afficher]

import numpy as np
import matplotlib.pyplot as plt

def triangle(a,b,c):
    ab = round(np.linalg.norm(b-a), 1)
    bc = round(np.linalg.norm(c-b), 1)
    ca = round(np.linalg.norm(a-c), 1)
    P1 = np.concatenate((a,b), axis = 1)
    P2 = np.concatenate((c,a),axis = 1)
    P = np.concatenate((P1,P2),axis = 1)


    plt.plot(P[0,:],P[1,:],'bo-')
    plt.axis([np.min(P[0:])-1, np.max(P[1,:])+1, np.min(P[1,:])-1, np.max(P[1,:])+1])

    e=0.1


    plt.text(a[0]-e,a[1]+e, "A",fontsize = 15, fontweight = 'bold')
    plt.text(b[0]-e,b[1]+e, "B",fontsize = 15, fontweight = 'bold')
    plt.text(c[0]-e,c[1]+e, "C",fontsize = 15, fontweight = 'bold')

    plt.text((b+a)[0]/2 -e,(b+a)[1]/2 +e, "ab =" + str(ab))
    plt.text((b+c)[0]/2 -e,(b+c)[1]/2 +e, "bc =" + str(bc))
    plt.text((c+a)[0]/2 -e,(c+a)[1]/2 +e, "ca =" + str(ca))


    return(ab,bc,ca)



if __name__ == '__main__':
    a = np.array([[1,0]]).T
    b = np.array([[3,5]]).T
    c = np.array([[-1,6]]).T
    print(triangle(a,b,c))

L1. On importe numpy avec l'alias np pour l'utilisation et la création des tableaux array.
L2. On importe matplotlib.pyplot avec l'alias plt pour l'affichage.

L4. On définit la fonction triangle utilisant trois paramètres: a,b et c.
L5. à L7. On calcule les trois longueurs ab, bc et ca à l'aide de la fonction np.linalg.norm qui prend en paramètre le vecteur colonne correspondant au vecteur ab, bc ou ca (i.e. b-a, c-b ou a-c). On utilise également la fonction round qui prend en paramètre un nombre (ici la norme calculée) et le nombre de chiffres significatifs voulus pour l'affichage des longueurs. Ici on ne garde qu'un chiffre après la virgule.

L9. à L11. On concatène les points pour l'affichage : on fait un array correspondant à la liste des coordonnées des points suivants :
a, b, c, a. On y met la répétition de a pour relier le dernier coté du triangle.

L14. On affiche les points en les reliant à l'aide du tableau a, b, c, a crée précédemment.
L15. On définit les limites des axes pour un affichage plus sympa ( on définit ces limites en fonction des abscisses max et min, et des ordonnées max et min des points ).
L16. On crée un offset e qui correspondra à la translation des textes par rapport à leurs coordonnées pour les éloigner du triangle.

L18. à L20. On affiche les noms des points des côtés en gras.

L22. à L24. On affiche les longueurs des côtés du triangle.

L27. On renvoie les longueurs des côtés du triangle.

Voici ce que j'ai obtenu :

G6py34_resultat