♣ Exercice O1 :

        O1.1 : Créez un objet point qui a comme attributs ses coordonnées X et Y, puis créez une méthode permettant d'afficher l'objet.
Créez deux instances de cet objet et affichez-les.

Code copiable :[Afficher]

class Point(object):
    def __init__(self,x,y):
        self.X = x
        self.Y = y
       
    def __str__(self):
        return("Point ({0},{1})".format(self.X,self.Y))
       
if __name__ == '__main__':
    A = Point(1,3)
    B = Point(-5,10)
    print(A,B)

O1_1py34









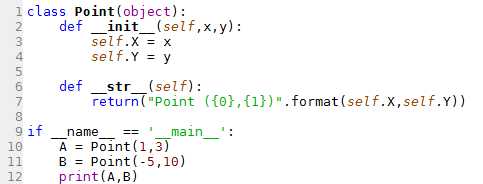
L1. On crée la classe Point qui hérite de object.
        L2. On définit le constructeur __init__ en mettant bien les paramètres self (l'instance créée), x (la première coordonnée), et y (la seconde coordonnée).
               L3. On définit la variable d'instance X égale à la première coordonnée.
               L4. De même pour la seconde coordonnée Y.

        L6. On définit la méthode pour afficher correctement l'instance objet.
               L7. Cette méthode renvoie une chaine de caractères qui sera affichée lors d'un appel à la fonction print.

L9. Si on lance le programme :
        L10. On crée une première instance nommée A dont les coordonnées sont 1 et 3.
        L11. On en crée une seconde nommée B de coordonnées -5, 10.
        L12. On affiche les deux points A et B. Voici ce qu'on obtient dans la console : Point (1,3)  Point (-5,10)


       O1.2 : Créez une méthode qui test l'égalité entre l'instance point et un autre point. Testez cette fonctionnalité.

Code copiable : [Afficher]

class Point(object):
    def __init__(self,x,y):
        self.X = x
        self.Y = y
       
    def __str__(self):
        return("Point ({0},{1})".format(self.X,self.Y))
       
    def __eq__(self,P):
        return(  (self.X == P.X)&(self.Y == P.Y) )     
       
       
if __name__ == '__main__':
    A = Point(1,3)
    B = Point(-5,10)
    Abis = Point(1,3)
    assert A == Abis
    assert A != B

O1_2py34

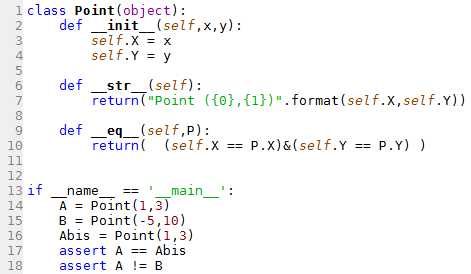
L1 à L8. Cf O1.1

    L9. On définit la méthode pour tester une égalité entre l'instance (self) et le point P.
         L10. Les deux points sont égaux si leurs coordonnées sont égales (i.e. que leurs variables X sont égales et que leurs variables Y sont égales). On renvoie donc True dans ce cas, et False sinon.

L13. Si on lance le programme :
        L14. On crée une première instance nommée A dont les coordonnées sont 1 et 3.
        L15. On en crée une seconde nommée B de coordonnées -5, 10.
        L16. On en crée un point Abis avec les mêmes coordonnées que celle de A.
        L17. A == Abis doit renvoyer True, donc on écrit une ligne assert qui nous renvoie une erreur si ce n'est pas le cas.
        L18. A != B doit nous renvoyer True, donc on écrit une ligne assert qui nous renvoie une erreur si ce n'est pas le cas.


      O1.3 :
Créez un objet Segment qui a comme attributs ses deux points aux extrémités (A et B pour le segment [AB]), puis :
- gérez l'affichage des instances,
- créez une méthode Pcenter qui renvoie le centre du segment (i.e. le point C pour l'instance [AB]),
- créez une méthode bisect qui renvoie les deux segments moitiés (i.e.[AC] et [CB] pour l'instance [AB]),
- créez une méthode qui test l'égalité entre deux segments.


Code copiable : [Afficher]
from Point import*

class Segment(object):
    def __init__(self,point1,point2):
        self.E1 = point1
        self.E2 = point2
       
    def __str__(self):
        return("Segment de {0} à {1}".format(self.E1,self.E2))
       
    def Pcenter(self):
        x =  (self.E1.X + self.E2.X)/2
        y = (self.E1.Y + self.E2.Y)/2
        return( Point(x,y) )
   
    def bisect(self):
        M = self.Pcenter()
        S1 = Segment(self.E1, M)
        S2 = Segment(M, self.E2)
        return(S1,S2)
       
    def __eq__(self,Seg):
        return( (self.E1 == Seg.E1)&(self.E2 == Seg.E2)|(self.E2 == Seg.E1)&(self.E1 == Seg.E2) )
       
       
       
if __name__ == '__main__':
    A = Point(-1,5)
    B = Point(2,3)
    Seg = Segment(A,B)
    print(Seg)
    assert Seg.Pcenter() == Point(0.5,4.0)  
    S1,S2 = Seg.bisect()
    print(S1,'\n',S2)

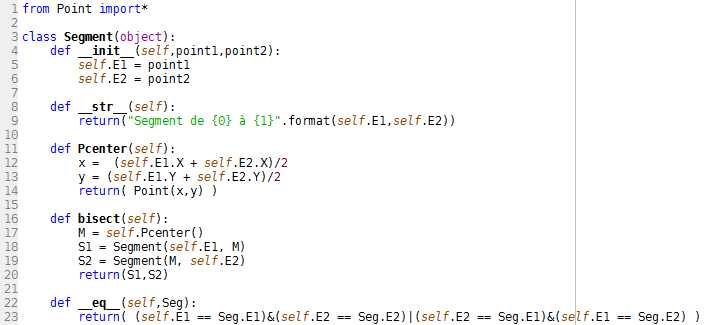
O1_3py34














L1. On importe la classe Point précédemment créée car elle sera utilisée pour les attributs de la classe Segment.

L3. On définit la classe Segment qui hérite de object.
        L4. On définit les instances Segment à l'aide de ce constructeur et des arguments point1 et point2 correspondant aux extrémités du segment.
                L5. La première extrémité est nommée E1 et correspond à l'argument point1 du constructeur.
                L6. La seconde extrémité est nommée E2 et correspond à l'argument point2 du constructeur.

        L8. On définit l'affichage des instances Segments. Pour cela on affiche une chaîne de caractères utilisant l'affichage des points correspondants aux extrémités du segment (i.e utilisant la méthode __str__ des instances Point).

 L11. On définit la méthode Pcenter :
               L12. On calcule l'abscisse du centre du segment : il s'agit de la moitié de la somme des abscisses des extrémités.
               L13. De même pour l'ordonnée.
               L14. On renvoie le point correspondant à ces coordonnées.

       L16. On définit la méthode bisect :
               L17. On récupère le point M, centre du segment à l'aide de la méthode Pcenter définie précédemment.
               L18. On définit le premier segment S1 : l'une de ses extrémités est le point M (centre du grand segment), et l'autre est une extrémité du grand segment.
               L19. De même pour le second segment S2.
               L20. On renvoie les deux segments.

      L22. On définit l'égalité entre deux segment,
              L23. comme étant l'égalité de ses extrémités sans prendre en compte l'ordre dans lequel on les regarde.



      O1.4 : Complétez la classe Segment avec une méthode qui calcule la longueur du segment.
Soient A = Point(1,5), B = Point(-5,3), C = Point(1,0), et D = Point(0.2,36).
Affichez la longueur des segments [AB], [BC] et [CD].

Code copiable :[Afficher]

from Point import*
import numpy as np

class Segment(object):
    def __init__(self,point1,point2):
        self.E1 = point1
        self.E2 = point2
       
    def __str__(self):
        return("Segment de {0} à {1}".format(self.E1,self.E2))
      
    def norm(self):
        Nx = abs(self.E1.X - self.E2.X)
        Ny = abs(self.E1.Y - self.E2.Y)
        return(np.sqrt(Nx**2 + Ny**2))       
       
    def Pcenter(self):
        x =  (self.E1.X + self.E2.X)/2
        y = (self.E1.Y + self.E2.Y)/2
        return( Point(x,y) )
   
    def bisect(self,n=2):
        M = self.Pcenter()
        S1 = Segment(self.E1, M)
        S2 = Segment(M, self.E2)
        return(S1,S2)
       
    def __eq__(self,Seg):
        return( (self.E1 == Seg.E1)&(self.E2 == Seg.E2)|(self.E2 == Seg.E1)&(self.E1 == Seg.E2) )

if __name__ == '__main__':
#    A = Point(-1,5)
#    B = Point(2,3)
#    Seg = Segment(A,B)
#    print(Seg)
#    assert Seg.Pcenter() == Point(0.5,4.0) 
#    assert Seg.norm() == np.sqrt(13)
#    S1,S2 = Seg.bisect()
#    print(S1,'\n',S2)
    A = Point(1,5)
    B = Point(-5,3)
    C = Point(1,0)
    D = Point(0.2,36)
    print("||AB|| = {0}\n||BC|| = {1}\n||CD|| = {2}".format(Segment(A,B).norm(), Segment(B,C).norm(),Segment(C,D).norm()))

O1_4py34
On définit la méthode norm dans la classe Segment. Elle s'applique à une instance (self).
On calcule Nx et Ny i.e les <--> de l'aide, i.e. les longueurs selon X et Y.
Puis on renvoie la racine de la somme des carrés (cf. Aide dans la page de l'énoncé).

Pour obtenir la longueur des segments :
1 - On crée les points A, B, C et D.
    A = Point(1,5)
    B = Point(-5,3)
    C = Point(1,0)
    D = Point(0.2,36)
2 - On crée les segments associés.
   AB = Segment(A,B)
   BC = Segment(B,C)
   CD = Segment(C,D)
3- On affiche la norme des segments.
   print(AB.norm())
   print(BC.norm())
   print(CD.norm())
  

Voici ce que j'ai obtenu :
||AB|| = 6.324555320336759
||BC|| = 6.708203932499369
||CD|| = 36.00888779176608


       O1.5 : Modifiez la méthode bisect de la classe pour qu'elle puisse découper un segment en plusieurs segments (rajoutez un paramètre n, égal à 2 par défaut et correspondant au nombre de segments voulus).

Code copiable : [Afficher]
from Point import*
import numpy as np

class Segment(object):
    def __init__(self,point1,point2):
        self.E1 = point1
        self.E2 = point2
       
    def __str__(self):
        return("Segment de {0} à {1}".format(self.E1,self.E2))
    
    def __eq__(self,Seg):
        return( (self.E1 == Seg.E1)&(self.E2 == Seg.E2)|(self.E2 == Seg.E1)&(self.E1 == Seg.E2) )
               
    def norm(self):
        Nx = abs(self.E1.X - self.E2.X)
        Ny = abs(self.E1.Y - self.E2.Y)
        return(np.sqrt(Nx**2 + Ny**2))       
       
    def Pcenter(self):
        x =  (self.E1.X + self.E2.X)/2
        y = (self.E1.Y + self.E2.Y)/2
        return( Point(x,y) )
   
    def bisect(self,n=2):
        dx = (self.E2.X - self.E1.X)/n
        dy = (self.E2.Y - self.E1.Y)/n
        x, y = self.E1.X, self.E1.Y
        L = []
        while n > 0:
            x,y = x + dx, y + dy
            L.append(Segment(Point(x -dx,y-dy),Point(x,y)))
            n -= 1
        return(L)

O1_5py34







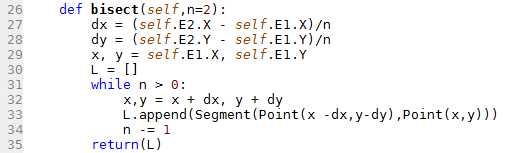
L26. On met n en paramètre de la méthode bisect, avec une valeur par défaut de 2.
L27. On calcule le pas dx correspondant à la longueur des n segments composant self selon x. (cf Aide)
L28. On calcule le pas dy correspondant à la longueur des n segments composant self selon y. (cf Aide)
L29. On récupère les coordonnées de la première extrémité de self dans x et y.
L30. On initialise le liste des segments composant self à une liste vide.
L31. Boucle While : Tant que n est strictement supérieur à 0,
L32.         On place les coordonnées de l'extrémité du segment suivant dans x et y, i.e x + dx et y + dy.
L33.         On ajoute le segment formé par l'extrémité précédente (i.e. (x-dx, y-dy)) et l'extrémité actuelle ( i.e. (x,y)) dans la liste L.
L34.         On décrémente n.
        Fin boucle While. Une fois sortie de la boucle while, nous avons créé et ajouté dans L les n segment de même longueur composants self.
L35. On renvoie L.



    O1.6 : Créez une méthode tri_equ qui à partir de l'instance segment renvoie deux segments qui forment un triangle équilatéral avec le segment.


Code copiable : [Afficher]
from Point import*
import numpy as np
import time

class Segment(object):
    def __init__(self,point1,point2):
        self.E1 = point1
        self.E2 = point2
       
    def __str__(self):
        return("Segment de {0} à {1}".format(self.E1,self.E2))
    
    def __eq__(self,Seg):
        return( (self.E1 == Seg.E1)&(self.E2 == Seg.E2)|(self.E2 == Seg.E1)&(self.E1 == Seg.E2) )
               
    def norm(self):
        Nx = abs(self.E1.X - self.E2.X)
        Ny = abs(self.E1.Y - self.E2.Y)
        return(np.sqrt(Nx**2 + Ny**2))       
       
    def Pcenter(self):
        x =  (self.E1.X + self.E2.X)/2
        y = (self.E1.Y + self.E2.Y)/2
        return( Point(x,y) )
   
    def bisect(self,n=2):
        dx = (self.E2.X - self.E1.X)/n
        dy = (self.E2.Y - self.E1.Y)/n
        x, y = self.E1.X, self.E1.Y
        L = []
        while n > 0:
            x,y = x + dx, y + dy
            L.append(Segment(Point(x -dx,y-dy),Point(x,y)))
            n -= 1
        return(L)
   

    def tri_equ(self):
        theta = np.arctan2(self.E2.Y - self.E1.Y, self.E2.X - self.E1.X)
        p = Point(self.E1.X + self.norm()*np.cos(theta+np.pi/3),self.E1.Y + self.norm()*np.sin(theta+np.pi/3))
        return(Segment(self.E1,p), Segment(p,self.E2))
   
O1_6py34




L38. On définit la méthode tri_equ dans la classe Segment.
        L39. On définit theta, l'angle formé par |E1E2| et l'axe des abscisses. Pour la formule : cf l'aide de l'énoncé.
        L40. On définit le point P. Pour les formules : cf l'aide de l'énoncé.
        L41. On renvoie les deux segments : |E1P| et |PE2|.



        O1.7 : Créez une fonction affiche qui prend en paramètre une liste L de segments et qui affiche les segments de la liste à l'aide de matplotlib.pyplot.


Code copiable :[Afficher]

def affiche(L):
    import matplotlib.pyplot as plt
    plt.clf()
    abscisse = []
    ordonnee = []
    for seg in L:
        abscisse.append(seg.E1.X)
        abscisse.append(seg.E2.X)
        ordonnee.append(seg.E1.Y)
        ordonnee.append(seg.E2.Y)
    plt.plot(abscisse,ordonnee,'bo-')
    plt.axis([0,1,0,1])
    plt.pause(0.01)

if __name__ == '__main__':
    A = Point(-1,5)
    B = Point(2,3)
    Seg = Segment(A,B)
    S1,S2,S3 = Seg.bisect(n=3)
    print(S1,'\n',S2,'\n',S3)
    affiche([S1,S2,S3])

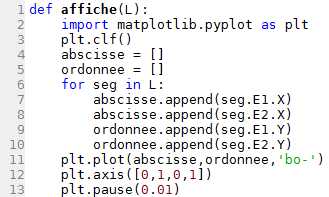O1_7py34L1. On définit la fonction affiche qui prend en paramètre une liste L.
        L3. On nettoie les graphiques préexistants,
        L4. et L5. On crée la liste abscisse et ordonnee, initialisées à []. Elles représentent la liste des points à afficher.
        L6.  Boucle for : Pour tous segments contenus dans la liste L :
                L7. et L8. On ajoute, dans la liste des abscisses des points à afficher, les abscisses des extrémités du segment.
                L9. et L10. On ajoute, dans la liste des ordonnées des points à afficher, les ordonnées des extrémités du segment.
        L11. Une fois la liste L entièrement parcourue, on peut afficher les listes créées.


       


        O1.8 : Créez une fonction Koch qui affiche des flocons de Koch à l'aide des classes créées précédemment.

Code copiable : [Afficher]

def Koch(L,n=6):
    while n > 0:
        futur_L = []
        for i in range(len(L)):
            currentS = L[i]
            S1,S2,S3 = currentS.bisect(n=3)
            S2bis,S2ter = S2.tri_equ()
            futur_L += [S1,S2bis,S2ter,S3]
        affiche(futur_L)
        L = futur_L
        n = n-1

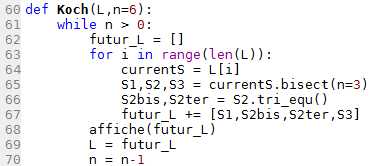 O1_8Pour obtenir des flocons de Koch comme ci-dessous : Koch([Segment(Point(0,0),Point(1,0))])
Koch








L60. On crée la fonction Koch qui a comme paramètres :
              - la liste L des segments avec lesquelles on fera des flocons,
              - le nombre n de découpes à effectuer.
        Boucle While : L61. Tant que le nombre de découpes restantes est supérieur à 0,
                L62. On initialise le liste futur_L à une liste vide, elle contiendra les nouveaux segments à utiliser.
                Boucle For : L63. Pour tous les segments de L,
                        L64. On récupère le segment dans la variable currentS,
                        L65. On découpe ce segment en trois segments S1, S2 et S3 à l'aide de la méthode bisect (exercice O1_5). Attention, il est important de mettre le paramètre n à 3 pour obtenir 3 segments !
                        L66. On applique la méthode tri_equ (exercice O1_6) sur S2 ce qui nous renvoie les deux segments S2bis et S2ter formant un triangle équilatéral avec S2.
                        L67. On place dans la liste futur_L:
                                                      - S1, premier segment de la découpe en trois.
                                                      - S2bis, premier segment formant un triangle équilatéral avec le deuxième segment de la découpe en trois.
                                                      - S2ter, second segment formant un triangle équilatéral avec le deuxième segment de la découpe en trois.
                                                      - S3, troisième segment de la découpe en trois.
                Fin boucle For : L68. Une fois la liste L entièrement parcourue (i.e. tous les segments ont été traités), on dessine les nouveaux segments à l'aide de la fonction affiche (exercice O1_7).
                L69. La liste L est mise à jour.
                L70. On décrémente n.



♣ Exercice O2 :

        O2.1 : Un plateau de jeu est un quadrillage de plusieurs cellules caractérisées par un état (vivant ou mort) et par leur positions (x,y) sur le plateau ci-contre.
Un plateau de jeu a une taille variable, mais quoi qu'il arrive la cellule en bas à gauche du tableau est celle de position (0,0).
Créez deux classes Board et Cell respectant ce contexte. Faites attention à bien ranger l'ensemble des cellules d'un plateau en attribut du plateau !
 

Code copiable :[Afficher]
class Board(object):
    def __init__(self,xMax=10,yMax=10):
        self.xMax = xMax
        self.yMax = yMax
        self.cells = self.createCells()
       

    def createCells(self):
        cells = []
        for x in range(0,self.xMax+1):
            X = []
            for y in range(0,self.yMax+1):
                X.append(Cell(x,y))
            cells.append(X)
        return(cells)
       
       
       
class Cell(object):
    def __init__(self,x,y,alive = False):
        self.x = x
        self.y = y
        self.alive = alive
       
Classe Cell
O2_1py34
Pour l'instant les instances de Cell n'ont besoins d'être définie qu'avec trois attributs :
- la position en abscisse de la cellule (x),
- la position en ordonnée de la cellule (y),
- son état (alive, égale à True si la cellule est vivante, et à False si elle est morte)
Ici, la création d'une cellule se fait de la manière suivant : cellule = Cell(3,2) pour une cellule morte de position (3,2)

Classe Board
O2_1bispy34
L1. à L5. Un plateau possède trois attributs.
- sa longueur en abscisse (xMax, égal à 10 par défaut),
- sa longueur en ordonnée (yMax, égal à 10 par défaut),
- l'ensemble de ses cellules (cells) crée par la méthode createCells. Voici la structure utilisé pour cet attribut :
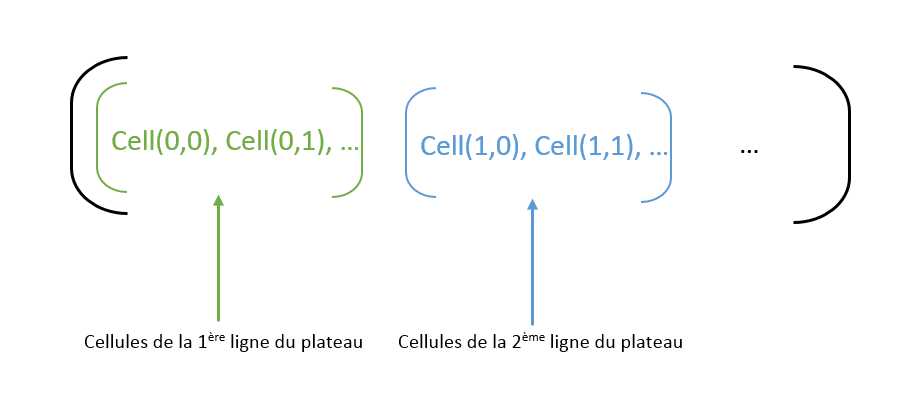
O2_1illustration












L8. On définit la méthode createCells.
        L9. On initialise la liste des lignes de cellules du tableau à une liste vide.
        Boucle For : L10. Pour toutes les lignes du tableau,
                  L11. On définit la liste des cellules de la ligne par une liste vide.
                Boucle For : L12. Pour toutes les colonnes du tableau,
                         L13. On crée une cellule de coordonnée (le numéro de la ligne, le numéro de la colonne) et on l'ajoute à la liste des cellules de la ligne.
                Fin de Boucle For : L14. On ajoute la liste des cellules de la ligne dans la liste des lignes de cellules du tableau.
        Fin de Boucle For
        L15. On renvoie la liste de liste.
              

       O2.2 : Pour chacune de ces classes, définissez la méthode __str__ (i.e. l'appel à la fonction print). Voici les exigences :
                 - print( ) pour une instance Board doit au moins afficher l'état de chacune des cellules de Board,
                 - print( ) pour une instance Cell doit afficher chacune de ses caractéristiques.


Code copiable :[Afficher]

class Board(object):
    def __init__(self,xMax=10,yMax=10):
        self.xMax = xMax
        self.yMax = yMax
        self.cells = self.createCells()

    def createCells(self):
        cells = []
        for x in range(0,self.xMax+1):
            X = []
            for y in range(0,self.yMax+1):
                X.append(Cell(x,y))
            cells.append(X)
        return(cells)
       
    def __str__(self):
        text = "Board :\n"
        for x in range(0,self.xMax+1):
            for y in range(0,self.yMax+1):
                value = self.cells[x][y].alive
                text += str(value) + "  "
                if value:
                    text += " "
            text += "\n"
        return(text)

class Cell(object):
    def __init__(self,x,y,alive = False):
        self.x = x
        self.y = y
        self.alive = alive
 
    def __str__(self):
        return("Cell :\n \tposition : (x,y) = ({0},{1}),\n\tstate : {2}".format(self.x,self.y,self.alive))
       
Classe Cell
O2_2py34
On redéfinit la fonction print à travers la définition de __str__. Ce que print affiche est ce que la __str__ renvoie.
Ici, un print d'une cellule affichera la position et l'état de la cellule à l'aide de ses attributs.

Classe Board
O2_2bispy34_Pour un plateau on affiche l'état de toute ses cellules.
L32. La chaîne de caractères renvoyée par __str__ est initialisée.
Boucle For : L33. Pour toutes les abscisses x des cellules du plateau,
                    Boucle For : L34. Pour toutes les ordonnées y des cellules du plateau,
                                          L35. La valeur à afficher est l'attribut 'alive' de la cellule de position x,y de la liste des cellules du plateau.
                                          L36. On ajoute la chaîne de caractères correspondant à cette valeur dans la variable text.
                                          L37. Si la valeur est True,
                                                        L38. alors on rajoute quelques espaces "  " pour que les valeurs restent alignées lors de l'affichage ("False" possède plus de lettres que "True").
                   Fin boucle for : L39. Arrivé ici, on a traité toutes coordonnées y pour un x fixé, donc on a traité une ligne ! On va donc à la ligne dans l'affichage.
Fin boucle for: L40. Arrivé ici, toutes les cellules ont été traitées. On renvoie donc la variable text.
                                              


       O2.3 : Créez une méthode dans la classe Cell qui permet d'inverser son état, puis créez une méthode dans la classe Board qui prend en paramètre une liste de cellules et qui change l'état de chacune de ces cellules.

Code copiable :[Afficher]
class Cell(object):
    def __init__(self,x,y,alive = False):
        self.x = x
        self.y = y
        self.alive = alive
   
    def changeState(self):
        self.alive = not self.alive
   
    def __str__(self):
        return("Cell :\n \tposition : (x,y) = ({0},{1}),\n\tstate : {2}".format(self.x,self.y,self.alive))


class Board(object):
    def __init__(self,xMax=10,yMax=10):
        self.xMax = xMax
        self.yMax = yMax
        self.cells = self.createCells()
       

    def createCells(self):
        cells = []
        for x in range(0,self.xMax+1):
            X = []
            for y in range(0,self.yMax+1):
                X.append(Cell(x,y))
            cells.append(X)
        return(cells)
       
    def changeCells(self,ListPos): #ListePos = [ [x1,y1], [x2,y2] ...]
        for pos in ListPos:
            self.cells[pos[0]][pos[1]].changeState()
       
    def __str__(self):
        text = "Board :\n"
        for x in range(0,self.xMax+1):
            for y in range(0,self.yMax+1):
                value = self.cells[x][y].alive
                text += str(value) + "  "
                if value:
                    text += " "
            text += "\n"
        return(text)

Classe Cell
O2_3py34Pour inverser l'état d'une cellule, il suffit d'inverser son attribut alive de type boolean (True ou False). Pour cela placer à côté de l'attribut not qui est une négation.
Ici la méthode pour changer l'état d'une cellule est définit par changeState( ).

Classe Board
O2_3py34bisPour changer l'état de plusieurs cellules d'un plateau, on définit la méthode changeCells( ) qui prend en paramètre la liste des coordonnées des cellules dont on veut modifier l'état. Les coordonnées doivent ici être écrites comme des listes de deux éléments [x,y] ou des tuples (x,y).
Pour tous les élements de la liste, on change l'état de la cellule de position x,y à l'aide de la méthode changeState( ) définie dans la classe Cell.


       O2.4 : Voici les deux étapes de cette partie :
- Créez une méthode dans la classe Board qui prend en paramètre une cellule et qui renvoie la liste des cellules voisines à celle-ci.
- Créez une méthode plot dans la classe Board qui permet d'afficher dans un graphique les cellules vivantes.

Code copiable : [Afficher]

class Board(object):
    def __init__(self,xMax=10,yMax=10):
        self.xMax = xMax
        self.yMax = yMax
        self.cells = self.createCells()
       

    def createCells(self):
        cells = []
        for x in range(0,self.xMax+1):
            X = []
            for y in range(0,self.yMax+1):
                X.append(Cell(x,y))
            cells.append(X)
        return(cells)
       
    def changeCells(self,ListPos):
        for pos in ListPos:
            self.cells[pos[0]][pos[1]].changeState()
       
    def __str__(self):
        text = "Board :\n"
        for x in range(0,self.xMax+1):
            for y in range(0,self.yMax+1):
                value = self.cells[x][y].alive
                text += str(value) + "  "
                if value:
                    text += " "
            text += "\n"
        return(text)
       
    def plot(self):
        plt.clf()
        for x in range(0,self.xMax+1):
            for y in range(0,self.yMax+1):
                if self.cells[x][y].alive:                   
                    plt.plot(y,x,"bo",mew = 5, ms = 15.0)
                    plt.axis([0,self.yMax,0,self.xMax])
       
    def neighbour(self,cell):
        L = []
        x = cell.x
        y = cell.y
       
        if x > 0 and y > 0:
            L.append(self.cells[x-1][y-1])
            L.append(self.cells[x-1][y])
            L.append(self.cells[x][y-1])
        elif x > 0:
            L.append(self.cells[x-1][y])
        elif y > 0:
            L.append(self.cells[x][y-1])
           
        if x < self.xMax and y < self.yMax:
            L.append(self.cells[x+1][y+1])
            L.append(self.cells[x+1][y])
            L.append(self.cells[x][y+1])
        elif x < self.xMax:
            L.append(self.cells[x+1][y])
        elif y < self.yMax:
            L.append(self.cells[x][y+1])
           
          
        if  x > 0 and  y < self.yMax:
            L.append(self.cells[x-1][y+1])
        if y > 0 and x < self.xMax:
            L.append(self.cells[x+1][y-1])
       
        return(L)

O2_4py34
Les cellules voisines :

Les cellules voisines se trouvent autour des coordonnées x,y :
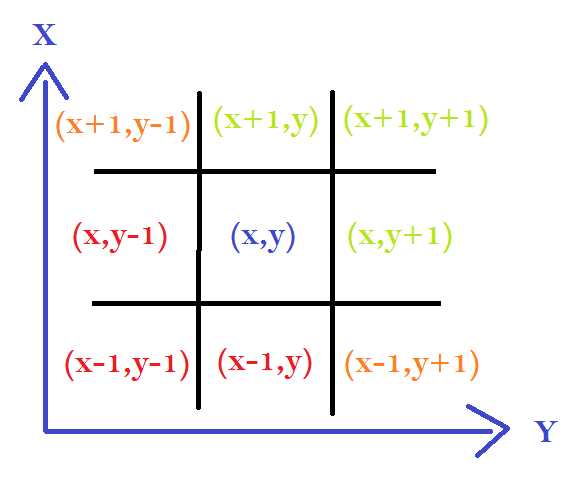
O2_4py34explication










Il faut vérifier que (x,y) ne se trouve pas en bord de plateau:
    - Si x et y sont strictement positif alors la cellule considérées n'est pas dans le coin gauche du plateau. Donc les coordonnées rouges sont des coordonnées de cellules voisines.
    - Cependant si x est la seule coordonnée strictement positive (i.e y < 0 ) alors la cellule est en bas du plateau, il ne faut pas considéré les cellules de coordonnées rouges se trouvant sur la ligne du bas.
    - De même, si seule y est strictement positive (i.e. x < 0) alors la cellule est sur le bord gauche du plateau, il ne faut pas considérés les cellules de coordonnées rouges se trouvant sur la colonne de gauche.

   - Si  (x,y) est strictement inférieur terme à terme aux dimensions du plateau alors c'est que la cellules n'est pas dans le coin en haut à droite du plateau. (coordonnées en vert)
   - si x < xMax mais que y est la valeur maximale, alors la cellule est sur le bord droit du plateau, il ne faut pas les cellules à droites de la cellule considérées n'existent pas.
 
(...)

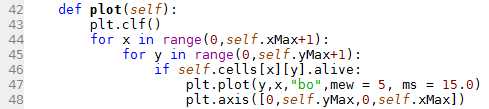O2_4py34bisL'affichage :
Boucle For : Pour toute les colonnes du plateau,
                     Boucle For : Pour toute les lignes du plateau,
                                        Si la cellule se trouvant à l'intersection de la ligne et de la colonne considérés est vivante,
                                                   On l'affiche avec un rond plein, bleu, et un contour noir.
                                                    On borne les axes ( ATTENTION : cette ligne devrait être mise à la fin de la fonction, en dehors des boucles)




       O2.5 : A l'aide des classes créées précédemment, implémentez le jeu de la vie en créant une méthode stepLife dans la classe Board qui réalise un incrément du jeu de la vie.

"À chaque étape, l'évolution d'une cellule est entièrement déterminée par l'état de ses huit voisines de la façon suivante :
Code copiable classe Board: [Afficher]

import matplotlib.pyplot as plt
import numpy as np

class Board(object):
    def __init__(self,xMax=10,yMax=10):
        self.xMax = xMax
        self.yMax = yMax
        self.cells = self.createCells()
       

    def createCells(self):
        cells = []
        for x in range(0,self.xMax+1):
            X = []
            for y in range(0,self.yMax+1):
                X.append(Cell(x,y))
            cells.append(X)
        return(cells)
       
    def changeCells(self,ListPos):
        for pos in ListPos:
            self.cells[pos[0]][pos[1]].changeState()
       
    def __str__(self):
        text = "Board :\n"
        for x in range(0,self.xMax+1):
            for y in range(0,self.yMax+1):
                value = self.cells[x][y].alive
                text += str(value) + "  "
                if value:
                    text += " "
            text += "\n"
        return(text)
       
    def plot(self):
        plt.clf()
        for x in range(0,self.xMax+1):
            for y in range(0,self.yMax+1):
                if self.cells[x][y].alive:                   
                    plt.plot(y,x,"bo",mew = 5, ms = 15.0)
                    plt.axis([0,self.yMax,0,self.xMax])
       
    def neighbour(self,cell):
        L = []
        x = cell.x
        y = cell.y
       
        #coin en bas à gauche (3cells)
        if x > 0 and y > 0:
            L.append(self.cells[x-1][y-1])
            L.append(self.cells[x-1][y])
            L.append(self.cells[x][y-1])
        elif x > 0:
            L.append(self.cells[x-1][y])
        elif y > 0:
            L.append(self.cells[x][y-1])
           
        #coin en droit haut(3cells)
        if x < self.xMax and y < self.yMax:
            L.append(self.cells[x+1][y+1])
            L.append(self.cells[x+1][y])
            L.append(self.cells[x][y+1])
        elif x < self.xMax:
            L.append(self.cells[x+1][y])
        elif y < self.yMax:
            L.append(self.cells[x][y+1])
           
           
        #deux autre coin (2cells)
        if  x > 0 and  y < self.yMax:
            L.append(self.cells[x-1][y+1])
        if y > 0 and x < self.xMax:
            L.append(self.cells[x+1][y-1])
       
        return(L)
           
       
    def stepLife(self):
        C = self.cells
        haveToChange = []
        for line in C:
            for cell in line:
                neighbour = self.neighbour(cell)
                counter = 0
                for ngb in neighbour:
                    if ngb.alive:
                        counter +=1
                if cell.alive:
                    if counter != 2 and counter !=3:
                        haveToChange.append([cell.x,cell.y])
                else:
                    if counter == 3:
                        haveToChange.append([cell.x,cell.y])
        self.changeCells(haveToChange)
Code copiable classe Cell : [Afficher]
class Cell(object):
    def __init__(self,x,y,alive = False):
        self.x = x
        self.y = y
        self.alive = alive
   
    def changeState(self):
        self.alive = not self.alive
   
    def __str__(self):
        return("Cell :\n \tposition : (x,y) = ({0},{1}),\n\tstate : {2}".format(self.x,self.y,self.alive))
       

Voici la méthode ajoutée dans le classe Board :
O2_5py34L85. On définit la méthode stepLife de la classe Board.
        L86. On place dans la variable C l'ensemble des cellules du plateau.
        L87. On place dans la variable haveToChange la liste des cellules dont l'état doit être inversé.
        Boucle For (x2) :  L88. et L89. Pour toutes les cellules du plateau,
                                       L90. On récupère la liste des cellules voisines,
                                       L91. On initialise le nombre de cellules voisines vivantes à 0.
                                       Boucle For : L92. Pour toutes les cellules voisines,
                                                            L93. et L94. si la cellule est vivante, alors on incrémente le compteur !
                                       Fin Boucle For : Ici, count est le nombre de cellules voisines vivantes que possède la cellule considérée.
                                       L95. Si la cellule considérée est vivante,
                                                            L96. et L97. Si elle ne possède ni 2 ni 3 cellules voisines vivantes alors elle doit mourir (changer d'état).
                                       L98. Mais si la cellule considérée n'est pas vivante,
                                                            L99. et L100. et qu'elle a exactement trois cellules voisines vivantes, alors elle doit naître (changer d'état).
Fin Boucle For (x2) : L101. Arrivé ici, la liste haveToChange correspond bien à la liste des cellules dont l'état doit changer. On applique donc la méthode changeCells de la classe Board à cette liste.


Pour lancer le jeu de la vie :

if __name__ == '__main__':
    b = Board(xMax=10,yMax=10)
    b.changeCells([[5,3],[4,4],[6,4],[4,5],[5,5],[6,5],[4,6],[6,6],[5,7]])
    b.plot()
    plt.pause(1)
    stop = 20
    for i in range(stop):
        b.stepLife()
        b.plot()
        plt.pause(1)