♣ Exercice S2 : L'exercice consiste à créer une fonction non récursive Fibo qui a pour paramètre un entier naturel n non nul et qui renvoie Un.





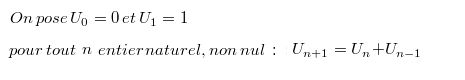
- Une solution fonctionnant sous Python 2.7 et Python 3.4 :





L8. Définition de la fonction Fibo de paramètre n.
L9. On définit U comme étant le premier terme de la suite, i.e. U0, i.e. 0.
L10. On définit UU comme le second terme de la suite, i.e. U1, i.e. 1.
L11. La variable i représente ici l'indice du dernier terme connu de la suite. Pour l'instant il s'agit de 1.

Boucle While : L12. Tant qu'on ne connait pas le terme Un de la suite, i.e. tant que l'indice i est strictement inférieur à n :
                        L13. On incrémente i (pour l'instant U est le terme d'indice i-1, et UU est le terme d'indice i-2)
                        L14. Et on garde en mémoire le dernier terme calculé car il faudra s'en servir pour redéfinir U qui prendra la valeur de UU. Pour cela on définit une variable intermédiaire nommée Save.
                        L15. On calcule le terme Ui avec la formule donnée dans la définition de la suite. UU prend la valeur de Ui.
                        L16. Il faut donc que U prenne la valeur de Ui-1, i.e. de Save.
Fin Boucle While : Une fois sorti de la boucle, UU est le terme d'indice n.

L17. Donc on renvoie UU.

---

♣ Exercice S3 : Reprenez la définition de la suite de Fibonacci donnée dans l'exercice précédent : l'exercice consiste à créer une fonction récursive FiboR qui a pour paramètre un entier naturel n et qui renvoie Un.



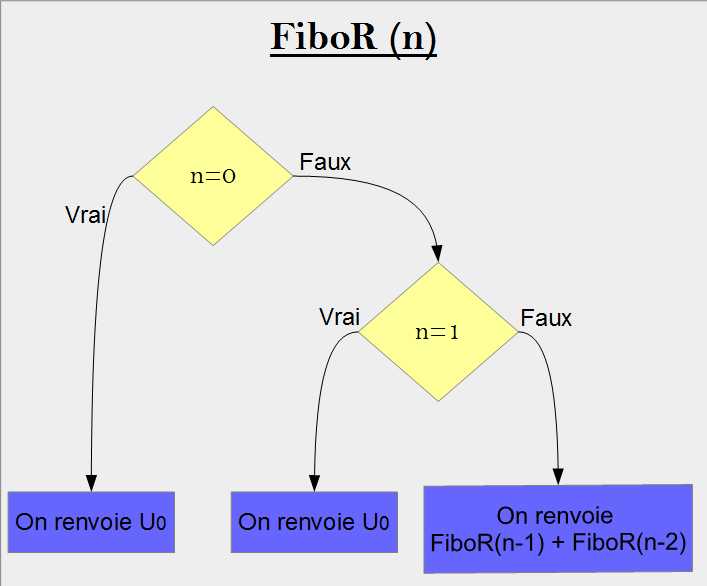
L1. On va définir la fonction FiboR de paramètre n.
L2. Si n est nul,
        L3. Alors il s'agit du calcul de U0, or U0=0. On renvoie donc 0.
L4. Si n est égal à 1,
        L5. Alors il s'agit du calcul de U1, or U1=1. On renvoie donc 1.
L6. Sinon
        L7. On retourne le calcul de Un, c'est-à-dire Un-1 + Un-2. Or Un= FiboR(n), donc on renvoie FiboR(n-1) + Fibo(n-2).

---

♣ Exercice S5 : Le  nombre d'or est la limite de la suite notée Vn et définie à partir de la suite Un de Fibonacci. Voici comment on les définit :

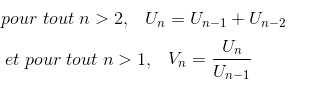
On prend V1=0,  U1=1 et U0=0.
L'exercice consiste à créer une fonction nbr_or qui a pour paramètre un nombre e strictement inférieur à 1, et qui renvoie une approximation de la valeur du nombre d'or avec une précision e.


-une solution fonctionnant sous Python 2.7.5 et Python 3.4




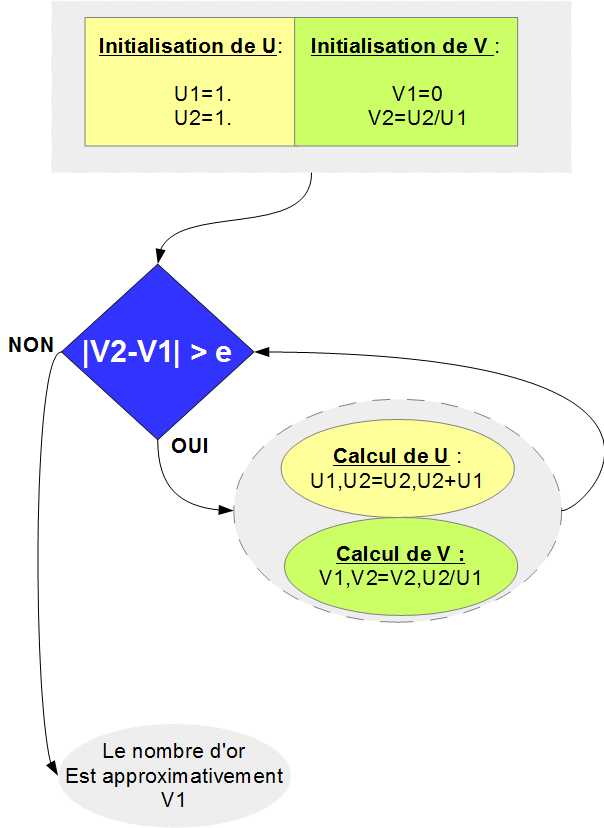
L1. On définit la fonction nbr_or ayant pour paramètre e.
L2. à L5. On initialise U (U1=1 et U2=2) et V (V1=0 et V2=U2/U1 par définition).
Boucle While :  L6. Tant que la différence entre les deux termes consécutifs de V est, en valeur absolue, strictement supérieure à e,
                          L7. On calcule les nouveaux U1 et U2 : pour cela, on place la valeur de U2 en U1 et on place l'ancienne valeur de "U2 + la valeur de U1" dans U2.
                          L8. On calcule les nouveaux V1 et V2 : pour cela, on place la valeur de V2 dans V1, et la valeur de U2/U1 dans V2.
Fin Boucle While : L9. Quand on est là c'est qu'on ne vérifie plus la condition |V2-V1| > e. On a donc un écart inférieur ou égal à e entre les deux termes consécutifs de V.
On renvoie donc V1, qui est l'approximation du nombre d'or.

---

♣ Exercice S6: On définit la suite Un de la façon suivante :

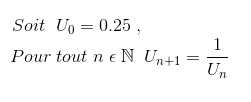
1) L'exercice consiste à créer une fonction U qui a pour paramètre un entier naturel n non nul et qui renvoie la liste des itérations de Un  : [U0, U1,..,Un,Un+1]
2) A partir de cette fonction, afficher un graphique représentant les 12 premiers termes de la suite Un en fonction de leurs indices.



-une solution fonctionnant sous Python 2.7.5 et Python 3.4
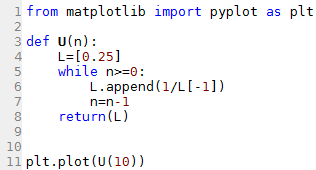
Code copiable : [Afficher]


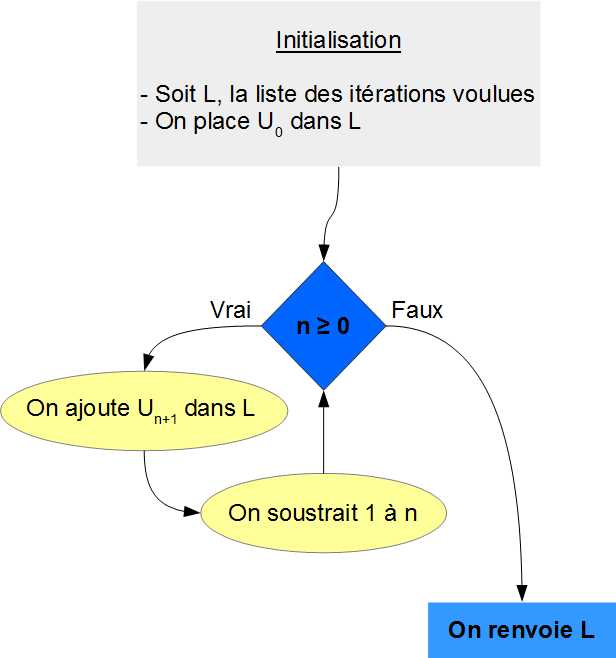
L1. On importe ce qu'il faut pour la question 2.

L3. On crée une fonction U qui a pour paramètre n.
L4. On crée une liste L composée de l'élément 0.25  (il s'agit de U0).
Boucle While: L5. Tant que le nombre d'éléments n à rajouter dans L est positif ou nul,
                        L6. On rajoute l'inverse du dernier élément de L dans la liste L à l'aide de la méthode append (il s'agit d'une itération de U),
                        L7. On décrémente n.
Fin Boucle While: Si on est ici c'est qu'on a calculé le bon nombre d'itérations.
                              L8. On renvoie L.

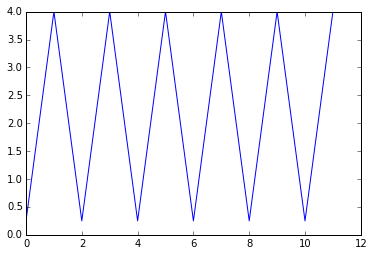
L11. On affiche le graphique demandé à l'aide de la fonction plot( ).
Voici ce que l'on obtient graphiquement :

---

♣ Exercice S7: Tracer Un(x) pour les différents entiers naturels n appartenant à l'intervalle [1 , 5], et pour tout x appartenant à l'intervalle [0 , 10].




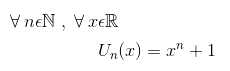
Voici une solution en accord avec l'aide proposée dans la page Exercices S :
Code copiable : [Afficher]
L1 - L2.  On importe numpy et matplotlib pour nous aider à créer la liste des abscisses et pour tracer les courbes demandées.

L6. On définit la fonction calculant la liste des images de X par Un.
        L7. On initialise L, la future liste des images de X par Un, à une liste vide.
        L8. On récupère la taille de X dans la variable taille à l'aide de la fonction len.
        Boucle for : L9. On parcourt la liste des X grâce aux indices des éléments de X ( i allant de 0 à taille -1).
                                    L10. On calcule l'image du i-ième élément de X par la fonction qui à x associe "x puissance n plus 1".
                                             On ajoute ce résultat à la fin de la liste L.
        Fin Boucle for :  Arrivé ici, on a rempli L de taille éléments.
        L11. On renvoie cette liste.

L13. On crée une liste de 20 réels compris entre 0 et 10 grâce à la fonction linspace de numpy  : linspace(start, stop, nombre d'éléments)

L15. On crée une figure sur laquelle on tracera toute les courbes désirées.
Boucle for : L16. Pour tous les entiers naturels n appartenant à l'intervalle [1,5],
                            L17- L18. On trace U(n,X) en fonction de X. Puis on fait une pause de 0.5 seconde à l'aide de la fonction pause de plt pour pouvoir observer le tracer s'effectuer.
Fin Boucle for : Arrivé ici, toutes les courbes demandées ont été tracées.