♣ Exercice V1 :
Dans cet exercice nous voulons enregistrer une simulation de jets de dé dans un fichier texte.
Créez un script python qui génère 500 jets de dé non pipé et qui écrit chaque résultat dans un fichier texte de nom name en suivant ces consignes :
        - une ligne par jet de dé,
        - numérotez les jets de dé,
        - utilisez une syntaxe comme :   "jet 52 : 2"
Créez ensuite une fonction count qui prend en paramètres le nom du fichier et un entier entre 1 et 6 inclus et qui renvoie le nombre de fois qu'il est apparu.
Grâce à cela vous pouvez afficher un "diagramme en bâtons" des fréquences d'apparition de chaque entier.

Pour le code copiable : 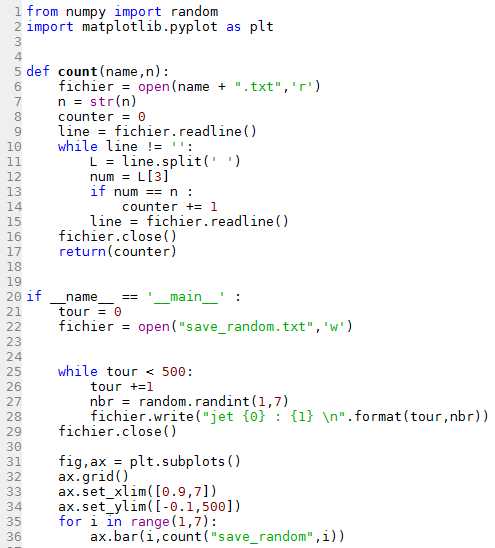V1py34___[Afficher]
from numpy import random
import matplotlib.pyplot as plt


def count(name,n):
    fichier = open(name + ".txt",'r')
    n = str(n)
    counter = 0
    line = fichier.readline()
    while line != '':
        L = line.split(' ')
        num = L[3]
        if num == n :
            counter += 1
        line = fichier.readline()
    return(counter)
       
       
if __name__ == '__main__' :
    tour = 0
    fichier = open("save_random.txt",'w')
   
   
    while tour < 500:
        tour +=1
        nbr = random.randint(1,7)
        fichier.write("jet {0} : {1} \n".format(tour,nbr))
    fichier.close()
   
    fig,ax = plt.subplots()
    ax.grid()   
    ax.set_xlim([0.9,7])
    ax.set_ylim([-0.1,500])
    for i in range(1,7):
        ax.bar(i,count("save_random",i))


☺La fonction count :
L1. On importe random de numpy pour la génération aléatoire de nombre.
L2. On importe matplotlib.pyplot pour le graphique. Ici on utilise plt comme alias.

L5. On définit d'abord les fonctions : ici, il n'y a que la fonction count qui prend en paramètres name (le nom du fichier) et n (l'entier recherché).
        L6. On ouvre le fichier en mode lecture avec la fonction open et le paramètre 'r'. Ici on doit compléter le nom du fichier par son extension (.txt). On concatène donc les deux chaines de caractères.
        L7. On transforme le nombre entier n en un string pour qu'on puisse le comparer avec des caractères.
        L8. On crée le compteur counter en l'initialisant à 0. Il indique le nombre d'apparitions de l'entier n.
        L9. On lit la première ligne du fichier à l'aide de readline() et on met la chaine de caractères obtenue dans line.
        Boucle While : L10. tant que la ligne n'est pas vide, i.e. que l'on n'est pas à la fin du fichier,
                                 L11. On crée une liste L dont les éléments sont des morceaux de la ligne. La découpe de la chaine de caractères line s'effectue avec la fonction split, ici on découpe dès que l'on trouve un espace '  '.
                                 L12. On récupère le numéro du dé L[3] car il se trouve en quatrième position dans la ligne .
                                 (on rencontre 3 espaces dans une ligne avant d'arriver sur le numéro du dé : "jet 25 : 2")
                                 L13. Si le numéro du dé est égal au numéro voulu (ici on compare bien deux chaînes de caractères)
                                              L14. Alors on incrémente le counter.
                                 L15. Mais quoi qu'il arrive, on lit la ligne suivante avec readline et on recommence le traitement.
          L16. Si on arrive ici c'est que le fichier texte a totalement été lu. On le ferme et on renvoie donc le nombre d'apparitions de n : counter.






☺Le script de génération de fichier :
L20. Cette ligne sert à ne pas appeler la suite du fichier lorsqu'il est simplement importé. Ce qu'il y a à la suite est appelé seulement si le fichier principal (main) est lui-même. Remarque : Elle n'est pas nécessaire dans ce contexte !
        L21. On crée le compteur tour en l'initialisant à 0. Il s'agira du nombre de lancés de dé déjà simulés.
        L22. On crée/ouvre le fichier "save_random.txt" en mode écriture 'w'. Il s'agit du fichier où l'on écrira le résultat de la simulation.

        Boucle While : L25. Tant qu'on n'a pas simulé nos 500 jets,
                                 L26. On incrémente le nombre de jets en incrémentant le compteur tour.
                                 L27. On génère un entier aléatoire entre 1 (inclus) et 7 (exclus) à l'aide de la fonction randint de random.
                                 L28. On écrit ce résultat dans le fichier. J'écris le résultat à l'aide de format qui me permet d'insérer des nombres dans une chaine de caractères. "\n" signifie retour à la ligne.
                                         Remarque : la syntaxe est équivalente à "jet " + str(tour) + " : " + str(nbr) + " \n"
        L29. Si on est là c'est que le traitement du fichier est terminé, on peut donc le fermer avec close().

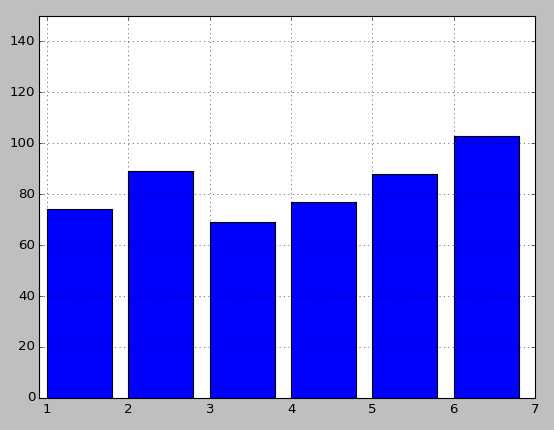
      V1py34_illustration

☺Le script pour afficher le graphique :
       L31. On crée une figure fig et un axe ax à l'aide de subplots. La figure correspond grossièrement à la fenêtre dans laquelle notre graphique va s'afficher, et notre ax au graphique en lui-même.
       L32. On fait apparaître une grille dans la fenêtre du graphique (pour pouvoir mieux visualiser les données).
       L33. On définit un intervalle pour l'axe des abscisses. Ici j'ai mis entre 0.9 et 7.
       L34. On fait de même pour l'axe des ordonnées.
       Boucle for : L35. Pour tout numéro qui peut potentiellement apparaître lors d'un lancé de dé, i.e tous les entiers allant de 1 (inclus) à 7 (exclus) :
                           L36. On affiche une barre commençant à l'abscisse i (le numéro du dé) et montant jusqu'à l'ordonnée correspondant au nombre d'apparitions de ce nombre dans le fichier texte save_random. Ici on fait donc appel à notre fameuse fonction count !




♣ Exercice V2 - Complément de V1 :
Deux joueurs lancent 500 fois le dé. Pour chaque numéro de 1 à 6, le joueur ayant le plus grand nombre d'apparition gagne 1 point (youpi !)
Simulez la partie et affichez les nombres d'apparitions des numéros. En déduire graphiquement le joueur qui a gagné.

Pour le code copiable : [Afficher]

from numpy import random
import matplotlib.pyplot as plt


def count(name,n):
    fichier = open(name + ".txt",'r')
    n = str(n)
    counter = 0
    line = fichier.readline()
    while line != '':
        L = line.split(' ')
        num = L[3]
        if num == n :
            counter += 1
        line = fichier.readline()
    fichier.close()
    return(counter)
       
def simulation_500(name):
    tour = 0
    fichier = open(name + ".txt",'w')
   
    while tour < 500:
        tour +=1
        nbr = random.randint(1,7)
        fichier.write("jet {0} : {1} \n".format(tour,nbr))
    fichier.close()
   
if __name__ == '__main__' :
    simulation_500("Cecile")
    simulation_500("Sophie")
   
   
    fig,ax = plt.subplots()
    ax.grid()   
    ax.set_xlim([0.9,7])
    ax.set_ylim([-0.1,500])
    width = 0.2
    for i in range(1,7):
        sim1 = ax.bar(i,count("Cecile",i),width = 0.2,color = "green")
        sim2 = ax.bar(i+width, count("Sophie",i),width = 0.2,color = "red")
    ax.legend( (sim1[0], sim2[0]), ('Cecile', 'Sophie') )

V1Cpy34J'ai modifié la script précédent :
- la fonction count est identique,
- la génération de simulation a été rangée dans une fonction nommée simulation_500, prenant en paramètre le nom du fichier d'enregistrement.

Ainsi, dans le script d'exécution, on exécute deux simulations : l'une qu'on enregistre dans le fichier Cecile.txt, et l'autre qu'on enregistre dans le fichier Sophie.txt.
Pour l'affichage on rajoute le paramètre width qui permet de gérer la largeur des barres. Ici les barres de la simulation de Cécile commencera au numéro voulu et aura une largeur de 0.2. Les barres de la simulation de Sophie commencera après celle de Cécile (donc décalées d'une largeur de barre).
On rajoute également le paramètre color pour définir la couleur des barres.

Puis, à la fin, on définit la légende pour plus de visibilité :
Cecile --> sim1 (barres vertes)
Sophie --> sim2 (barres rouges)

Voici l'un des résultat que j'ai obtenu :


V1_comp_illustration













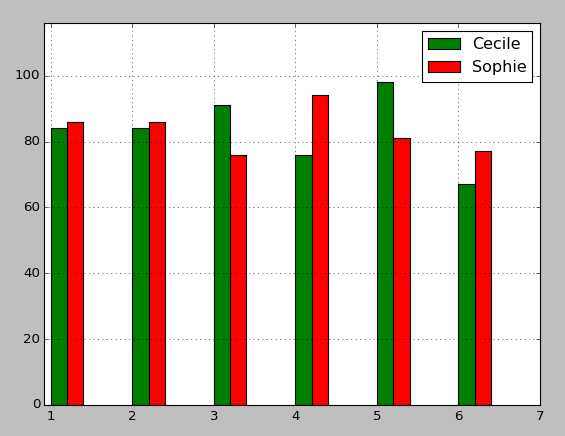
♣ Exercice V3 :
Créez un script qui : (Étape 1) génère deux nombres aléatoires,
                                  (Étape 2) demande à l'utilisateur le résultat de la multiplication des deux nombres,
                                  (Étape 3) vérifie le résultat et donne la correction si l'utilisateur à faux,
                                  (Étape 4) donne une note au bout de 10 tests.

Code copiable : [Afficher]
import random

nbr_max = 10
note = 0
for i in range(10):
    alea1 = random.randint(1,nbr_max)
    alea2 = random.randint(1,nbr_max)
    print("{0} x {1}".format(alea1,alea2))
    resultat = input("= " )

    if int(resultat) == alea1*alea2:
        print("Tres bien!\n")
        note+=1
    else:
        print("Non! c'est faux!, la reponse est ",alea1*alea2,"\n")
       
print("Voux avez ", note,"sur 10 !")

V3py34_












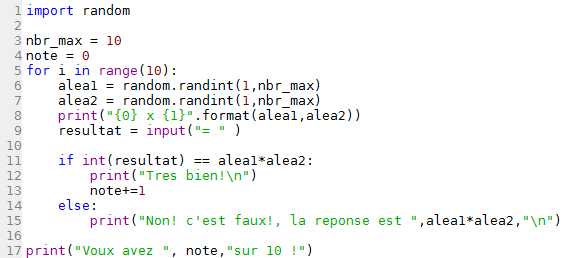
L1. On importe random pour les générations de nombres aléatoires.

L3. On met le nombre maximal que l'on peut générer dans la variable nbr_max, ici je l'ai mis à 10.
L4. On initialise la note à 0.
Boucle for : L5. Pour chaque test (i.e. 10 fois) :
                    L6. et L7. On génère deux nombres entiers entre 1 à nbr_max à l'aide de la fonction randint.
                    L8. On affiche les deux nombres en console sous la forme "nombre1 x nombre2" à l'aide de format.
                    L9. On demande à l'utilisateur d'entrer le résultat dans la console après la chaîne "= ".
                 
                    L11. On regarde si le nombre que l'utilisateur a rentré (une fois converti de string à integer à l'aide de int( )) est égal au produit des nombres générés. Si c'est le cas :
                              L12. et L13. On affiche le succès et on incrémente la note de 1 point.
                    L14. Sinon :
                                   L5. On affiche l'erreur et le résultat attendu.

L17. Une fois qu'on est sorti de la boucle for il est temps d'afficher la note !

♣ Exercice V4 :
Cet exercice se place dans le cadre des trinômes. Écrivez un script python qui pour les trois coefficients (a, b et c) d'un trinôme renvoie ses racines, les affiche et affiche la courbe correspondante.

Code copiable : [Afficher]
import numpy as np
import cmath
import matplotlib.pyplot as plt

def trinome(a,b,c):
    discr = b**2 -4*a*c
    if discr == 0 :
        return(-b/2*a,-b/2*a)
    elif discr > 0 :
        return((-b-np.sqrt(discr))/2*a, (-b + np.sqrt(discr))/2*a)
    else :
        return( -b-np.sqrt(abs(discr))*1j/2*a, -b + np.sqrt(abs(discr))*1j/2*a  )
    

if __name__ == '__main__':
    a,b,c = 1,-3,2
    x1, x2 = trinome(a,b,c)
    print("Les solutions de {0}x^2 + {1}x + {2} = 0 sont : {3} et {4}".format(a,b,c,x1,x2))
    
    if x1.imag == 0 :
        p = lambda x : a*x**2 + b*x + c
        X = np.arange( min(x1,x2)-1,max(x1,x2)+1,0.05)
        plt.plot(X,p(X))
        plt.plot(x1,p(x1),'o',color = "blue")
        plt.plot(x2,p(x2),'o', color = "blue")
        
        plt.title("Polynome {0}x^2 + {1}x + {2}".format(a,b,c))
        plt.grid()
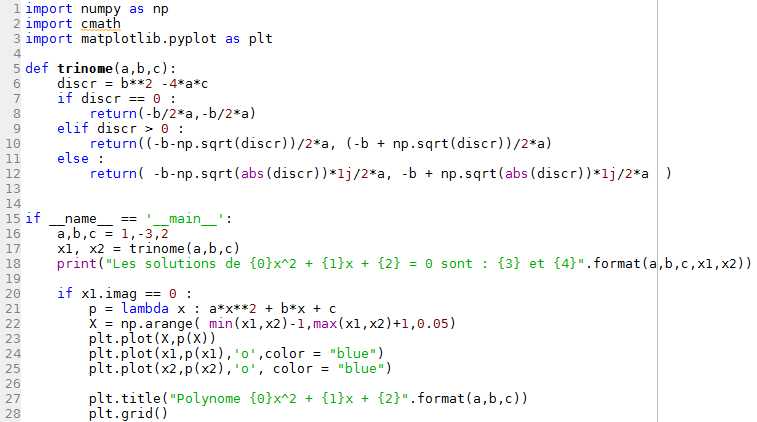V4py34_L1., L2. et L3. On importe numpy pour les calculs de racines carrés, cmath pour les nombres complexes, et matplotlib.pyplot pour l'affichage graphique.

L5. On définit la fonction trinôme qui prend trois nombres a, b et c en arguments.
        L6. On calcule le discriminant discr à l'aide de a, b et c.
        L7. S'il est nul,
                    L8. On renvoie deux fois la même racine.
        L9. S'il est strictement positif,
                    L10. On renvoie les deux racines réelles.
        L11. Sinon (i.e. s'il est strictement négatif),
                    L12. On renvoie les deux racines complexes en utilisant 1j pour la notation mathématique i.
    
L15. Cette ligne sert à ne pas appeler la suite du fichier lorsqu'il est simplement importé. Ce qu'il y a à la suite est appelé seulement si le fichier principal (main) est celui-ci.
        L16. On définit les trois nombres a, b et c correspondant aux coefficients du polynôme voulu.
        L17. On récupère les racines du polynôme avec la fonction trinome précédemment créée.
        L18. On affiche le trinôme et ses racines à l'aide de format.
   
        L20. Si les racines sont réelles, i.e. que la partie imaginaire (imag) est nulle :
                    L21. On définit le polynôme voulu à l'aide de lambda.
                    L22. On définit l'ensemble des abscisses qui nous intéressent : ici on veut afficher la fonction autour de ses racines.
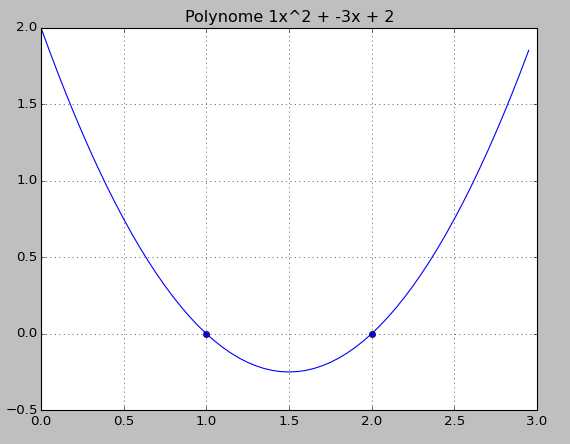
f6py34_resultat
                    L23. On affiche la fonction.
                    L24. et L25. On affiche les deux racines avec un point.

                    L27. On affiche le titre du graphique à l'aide de a, b et c.
                    L28. On affiche la grille pour mieux visualiser le graphique.