♣ Exercice f1 :
-Rappel de l'énoncé : L'exercice consiste à définir la fonction dicho qui a pour paramètres deux nombres a et b, une fonction f continue monotone sur [a,b] telle que f(a)*f(b) <0, et une précision e. Cette fonction doit renvoyer une approximation du zéro* de f ,appartenant à [a,b], avec une précision inférieure à e et par dichotomie.

* c'est-à-dire l'abscisse x telle que f(x)=0.

-une solution fonctionnant sous Python 2.7.5 et Python 3.4

L1. Définition de la fonction dicho avec les paramètres f,a,b et e.
L2. Au cas où l'utilisateur n'a pas mis a et b dans le bon sens on prend a comme étant le minimum entre a et b; et b le maximum.
Boucle While :  L3. Tant que l'intervalle [a,b] n'a pas une longueur inférieure à e, ( c'est-à-dire tel que (b-a) > e )
                          L4. On note m le milieu de l'intervalle [a,b].
                          L5. Si la fonction f s'annule entre b et m, c'est-à-dire si f(b) et f(m) ne sont pas du même signe (car f continue monotone sur [a,b]), ce qui équivaut à dire: si f(b)f(m) est négatif,
                          L6. Alors on réduit l'intervalle [a,b] à [m,b]. La variable a prend la valeur de m.
                          L7. Sinon (c'est-à-dire si f ne s'annule pas entre b et m)
                          L8. Alors cela signifie que f s'annule entre a et m. Donc on réduit l'intervalle [a,b] à l'intervalle [a,m]. La variable b prend la valeur de m.
Fin Boucle While : L9. On est sorti de la boucle While, donc on a la précision minimum voulue. On renvoie donc le milieu de l'intervalle [a,b] obtenu.

---

♣ Exercice f2 :
-Rappel de l'énoncé : L'exercice consiste à créer une fonction récursive facto qui a pour paramètre un entier naturel n et qui renvoie n! , c'est-à-dire n(n-1)(n-2)...3x2x1 .

-une solution fonctionnant sous Python 2.7.5 et Python 3.4

Aide : on se sert des conditions initiales 0!=1 et 1!=1
Voici l'explication de la correction suivante :







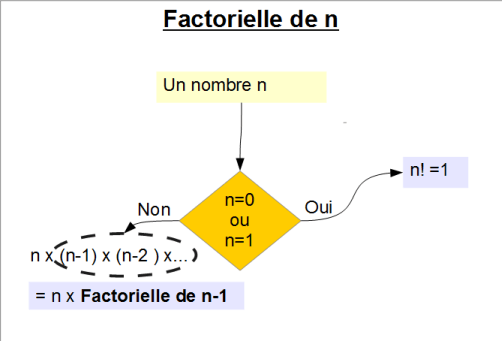
L1. La fonction qu'on va définir porte le nom facto et a pour paramètre n.
L2. Si n n'est ni 0 ni 1, c'est-à-dire s'il ne s'agit pas de définir les conditions initiales,
L3. Alors on retourne n fois facto (n-1).
L4. Sinon on est dans la définition des conditions initiales, c'est-à-dire dans le cas où n=0 ou n=1
L5. Et on retourne n! donc 1.

---

♣ Exercice f3 :
-Rappel de l'énoncé : L'exercice consiste à créer une fonction Euclide qui a pour paramètres deux entiers naturels non nuls a et b, et qui renvoie (en utilisant la méthode d'Euclide) le plus grand diviseur commun à a et à b.

-une solution fonctionnant sous Python 2.7.5 et Python 3.4



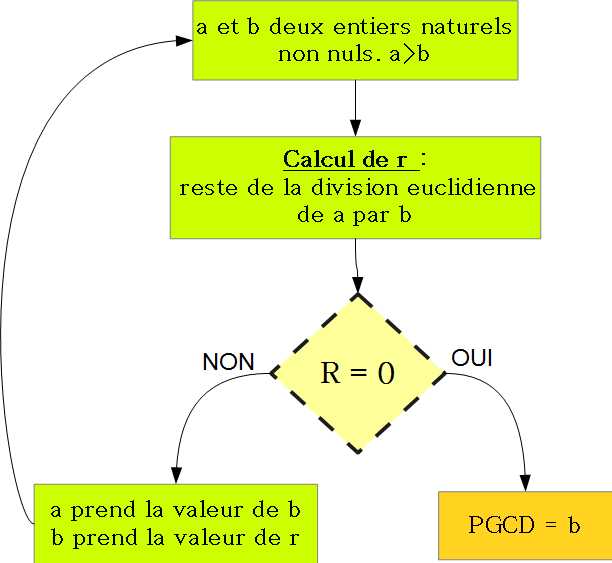
L1. Définition de la fonction portant le nom Euclide, et ayant deux paramètres nommés a et b.
L2. a reçoit le maximum entre les valeurs de a et de b, et b le minimum (ainsi la condition a > b ne pose pas de problème pour l'utilisateur).
L3. r reçoit le reste de la division euclidienne de a par b -on utilise l'opérateur %.
Boucle While : L4. tant que le reste r est non nul,
                         L5. r prend la place de b,
                         L6. b prend la place de a,
                         L7. et on recalcule le reste r de la division euclidienne du nouveau a par le nouveau b.
Fin Boucle While : Si on est là c'est que le reste r de la division euclidienne du a actuel par le b actuel est nulL8. On renvoie alors l'ancien reste, c'est-à-dire b.
                


Remarque : On aurait pu remplacer les deux lignes L5 et L6 par celle-ci : a,b=b,r

---

♣ Exercice f4 :
-Rappel de l'énoncé : Cet exercice consiste à créer une fonction convertDB qui a pour paramètre un entier naturel dec et qui renvoie la conversion de ce nombre en binaire.

-une solution fonctionnant sous Python 2.7.5 et Python 3.4
Code copiable : [Afficher]



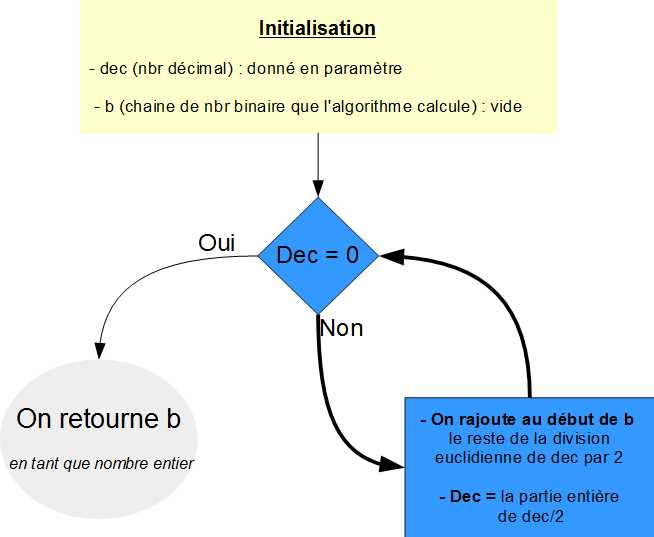
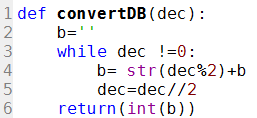
L1. On définit la fonction convertDB avec un paramètre nommé dec.
L2. On initialise b comme une chaîne de caractères vide ' '.
Boucle While : L3. Tant que le nombre dec est non nul,
                         L4. On recalcule b : il devient le reste de la division euclidienne (%) de dec par 2 auquel on a concaténé l'ancien b.
                         L5. On recalcule dec : il devient la partie entière de dec divisée par 2.
Fin Boucle While : L6. Lorsqu'on est là c'est qu'on a obtenu un coefficient dec nul. On renvoie donc b (converti en entier avec int()) qui est la concaténation des restes.

---

♣ Exercice f5 :
-Rappel de l'énoncé : Cet exercice consiste à créer une fonction convertBD qui a pour paramètre un nombre binaire b et qui renvoie la conversion de ce nombre en décimal.

Attention : ici on enlève tous les 0 à gauche du 1 le plus à gauche.
-une solution fonctionnant sous Python 2.7.5 et Python 3.4


 Code copiable : [Afficher]





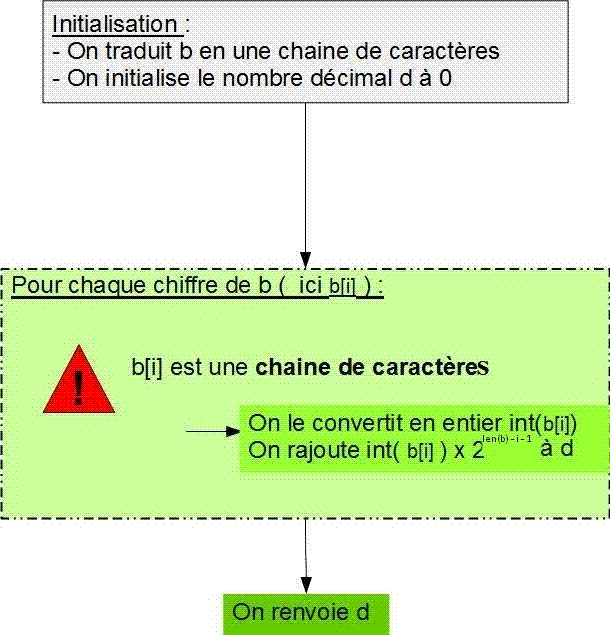
L1. On définit la fonction convertBD possédant un unique paramètre nommé b.
L2. On convertit b en une chaine de caractères à l'aide de la fonction str().
L3. On initialise une variable d à 0.

Boucle For : L4. Pour chaque i allant de 0 à la taille de b ( len(b) ), on s'intéresse à b[i].
                     L5. On rajoute à d la partie entière de b[i] ( int(b) )fois 2 puissance son indice len(b) - i - 1.
Fin Boucle For : Si on est ici c'est qu'on a parcouru tout le nombre binaire b.

                   L6. On renvoie d.

---

♣ Exercice f6 : Créez une fonction qui demande un nombre à l'utilisateur et affiche si ce nombre est pair ou impair.

Code copiable : [Afficher]
L2. On demande un entier à l'utilisateur à l'aide de la fonction input.
L3. On convertit ce que l'utilisateur nous a donné en un entier, car il s'agit d'un string et non d'un int.
L4. Si n est congru à 0 modulo 2, c'est-à-dire qu'il est divisible par 2, alors :
              L5. Il s'agit d'un nombre pair, donc on en informe l'utilisateur via l'affichage avec print.
L6. Sinon :
              L7. C'est qu'il s'agit d'un nombre impair.

---

♣ Exercice f7 : Soit x(t) qui a pour dérivée f(x(t))
Créez une fonction Euler qui a pour paramètres une fonction f, un intervalle de temps dt, un temps maximal tmax et la valeur initiale x, et qui renvoie la liste des valeurs de x(t) à l'aide de la méthode d'Euler.
Code copiable : [Afficher]
L1. On définit la fonction comme l'énoncé le demande.
L2. On crée la liste des valeurs de X, contenant la valeur initiale de x.
L3. On initialise la variable t à 0.1.
Boucle While : L4. Tant que cette valeur est inférieure à tmax :
                         L5. On calcule la valeur de x à l'aide de la méthode d'Euler,
                         L6. On ajoute cette valeur dans la liste X,
                         L7. Et on incrémente la variable t de la durée dt.
Fin boucle While : L8. Si on est là c'est que la variable temps est maximale, on renvoie donc la liste des valeurs de x.

---

♣ Exercice f8 :
-Rappel de l'énoncé : Créez une fonction maximum qui prend en paramètres 3 nombres et qui renvoie le plus grand d'entre eux.

Code copiable : [Afficher]

L1. On définit la fonction maximum et on nomme ses 3 paramètres a,b et c.
L2. Si a est supérieur à b et à c,
         L3. alors on renvoie a.
L4. Si on a plutôt b supérieur à a et à c,
        L5. alors on renvoie b.
L6. Sinon c'est que c est supérieur à a et à b,
       L7. alors on renvoie c.

Par exemple, maximum(0.1,5.2,6) nous renvoie 6