- Accueil
- Python: Exercices
- Exercices sur les listes
- Petit cours brouillon
- L1 : recherche d'un élément -
- L2 : maximum d'une liste ☆
- L3 : tri par sélection ★
- L4 : maximum elt par elt ★ ☆
- L5 : égalité entre listes ☆
- L6 : égalité entre listes (récursive) ★
- L7 : permutation ★
- L8 : simple manipulation -
- L9 : Opossum ★
- L10 : Split ☆
- L11 : Compréhension de listes ☆
- Corrections : Listes
- Exercices sur les fichiers
- Exercices sur les chaînes de caractères
- Petit cours brouillon
- C1 : recherche d'un caractère -
- C2 : remplacer un caractère ☆
- C3 : Compteur -
- C4 : Mélanger du texte ★
- C5 : Mélange interne ☆
- C6 : Mélange interne de phrase ☆
- C7 : Nombre d'occurence ★
- C8 : Présence d'un mot ★☆
- C9 : Suppression d'un mot ★
- C10 : Lettre <-> Nombre ★
- C11 : Rot13 ★☆
- C12 : Simple manipulation -
- C13 : Inversion ☆
- C14 : Prix d'achat ☆
- Corrections : Chaînes de caractères
- Exercices sur les suites
- Exercices sur les fonctions
- Exercices sur les matrices
- Exercices d'affichage
- Exercices de traitement d'images
- Exercices Vrac
- Exercices Orientés objets
- Exercices sur les listes
- Projets réalisés
- Historique
- Qui êtes-vous ?
->
Les solutions proposées ne sont pas forcément les meilleures ! Elles
peuvent même contenir des coquilles... C'est pourquoi je vous invite à
m'envoyer un commentaire pour toutes suggestions, critiques ou autres.
De même, votre propre correction et vos erreurs sont les bienvenues ! (quelque soit la version Python utilisée ou le langage)
De même, votre propre correction et vos erreurs sont les bienvenues ! (quelque soit la version Python utilisée ou le langage)
♣ Exercice M1 :
L'exercice consiste à créer une fonction diagdom qui a pour paramètre une matrice C carrée et qui renvoie True si la matrice est à diagonale dominante, ou False dans le cas contraire. (ici False et True sont des booléens, pas une chaîne de caractères)
- une solution fonctionnant sous Python 3.4 :
Code copiable : [Afficher]
def diagdom(C):
n = C.shape[0]
for i in range(n):
sum = 0
for j in range(n):
if j != i:
sum += abs(C[i][j])
if abs(C[i][i]) < sum:
return(False)
return(True)
n = C.shape[0]
for i in range(n):
sum = 0
for j in range(n):
if j != i:
sum += abs(C[i][j])
if abs(C[i][i]) < sum:
return(False)
return(True)
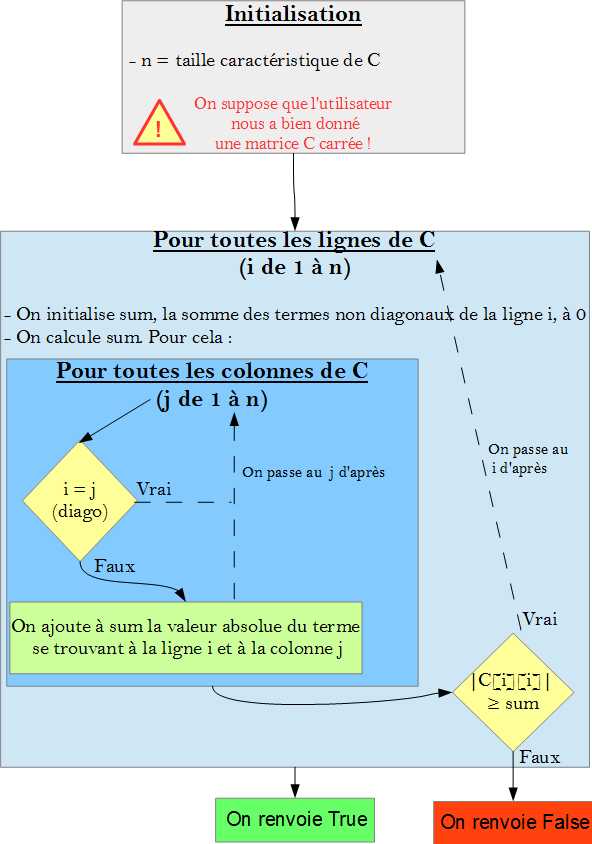

L1. On commence la définition de la fonction diagdom de paramètre C.
L2. On récupère le nombre de lignes (ou de colonnes) de C à l'aide de la méthode shape qui renvoie le tuple suivant : (nombre de lignes, nombre de colonnes) dont on ne récupère que le premier terme.
Boucle For : L3. On parcourt les lignes caractérisées par leurs numéros i allant de 1 à n.
L4. On initialise sum à 0 : il s'agira du terme de droite de l'inégalité (i fixé).
Boucle For : L5. On parcourt les colonnes caractérisées par leurs numéros allant de 1 à n.
=> Au final on parcourt les termes de la ligne i
L6. S'il ne s'agit pas d'un terme de la diagonale, i.e. si j n'est pas égal à i (numéro de ligne différent du numéro de colonne),
L7. On rajoute à sum la valeur absolue de ce terme.
L8. Ici, on conclut à propos de la vérification de l'inégalité pour une valeur de i. Si sum est supérieur à la valeur absolue du terme se positionnant à la fois sur la ligne i et sur la diagonale :
L9. Alors l'inégalité n'est pas vérifiée pour ce i : la matrice C n'est donc pas à diagonale dominante. On renvoie False.
L10. Si on est arrivé ici, c'est qu'on n'a jamais renvoyé False et qu'on a vérifié l'inégalité pour tout i. Donc la matrice est à diagonale dominante. On renvoie True.
♣ Exercice M2 :
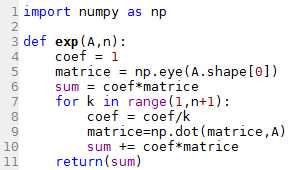
L'exercice consiste à créer une fonction exp non récursive qui a pour paramètres une matrice A carrée et un entier n et qui renvoie l'exponentielle de A à l'ordre n.
ATTENTION : La notation k est devenue n pour plus de simplicité.
Code copiable : [Afficher]
import numpy as np
def exp(A,n):
coef = 1
matrice = np.eye(A.shape[0])
sum = coef*matrice
for k in range(1,n+1):
coef = coef/k
matrice=np.dot(matrice,A)
sum += coef*matrice
return(sum)
def exp(A,n):
coef = 1
matrice = np.eye(A.shape[0])
sum = coef*matrice
for k in range(1,n+1):
coef = coef/k
matrice=np.dot(matrice,A)
sum += coef*matrice
return(sum)

♣ Exercice M4 :
L'exercice consiste à créer une fonction mult qui a pour paramètres deux matrices A et B et qui renvoie le produit matriciel AB (sans utiliser la fonction dot(A,B) qui renvoie déjà AB).
- une solution fonctionnant sous Python 3.4 :
Code copiable : [Afficher]
import numpy as np
def mult(A,B):
n,p = A.shape
q = B.shape[1]
C = np.zeros((n,q))
for i in range(n):
for j in range(q):
c = 0
for k in range(p):
c += A[i][k]*B[k][j]
C[i,j] = c
return(C)
def mult(A,B):
n,p = A.shape
q = B.shape[1]
C = np.zeros((n,q))
for i in range(n):
for j in range(q):
c = 0
for k in range(p):
c += A[i][k]*B[k][j]
C[i,j] = c
return(C)


L1. On importe numpy car cette bibliothèque nous servira à créer la matrice résultant du produit de A par B.
L3. On commence la définition de fonction en donnant un nom à la fonction et à ses deux paramètres.
L4. On récupère le nombre de lignes n et de colonnes p de A à l'aide de la méthode shape qui renvoie le tuple (n,p).
L5. On récupère le nombre de colonnes q de B.
L6. On initialise la matrice résultant du produit de A par B à une matrice nulle à l'aide de la méthode zeros.
==> C est de taille n x q car elle résulte du produit d'une matrice de taille n x p et d'une matrice de taille p x q.
Boucle For : L7. On caractérise les lignes de C par un numéro i. Pour tout i :
Boucle For : L8. On caractérise les colonnes de C par un numéro j. Pour tout j :
L9. On initialise le terme i,j de c à 0.
Boucle For : L10. Pour tout k (nombre caractérisant le numéro de la colonne dans laquelle on se place dans A, et la ligne dans laquelle on se place dans B)
L11. On rajoute à c le terme i,k de A fois le terme k,j de B.
Fin Boucle For (sur k) L12. On place c en i,j dans C.
Fin Boucle For (x2) L13. On renvoie la matrice C.
♣ Exercice M6 :
L'exercice consiste à créer une fonction pdtvecto qui a pour paramètres deux vecteurs X et Y à 3 coordonnées, et qui renvoie le produit vectoriel de X avec Y.
Code copiable : [Afficher]
import numpy as np
def pdtvecto(X,Y):
Z0 = X[1,0]*Y[2,0] - X[2,0]*Y[1,0]
Z1 = X[2,0]*Y[0,0] - X[0,0]*Y[2,0]
Z2 = X[0,0]*Y[1,0] - X[1,0]*Y[0,0]
return( np.array([[Z0,Z1,Z2]]) )
A = np.array([[0],[1],[2]])
B = np.array([[3],[5],[6]])
print( pdtvecto(A,B))
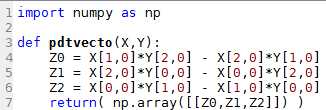
Attention ! Cette correction considère des vecteurs de type array( [ [a],[b],[c] ] ) de taille (3,1).
Attention aux indices !
♣ Exercice M7 :
Un chevalier et un martien vont au supermarché trois fois dans la semaine. Leurs nourrices voudraient savoir s'ils font attention aux prix.
A l'aide de la fonction np.linalg.solve, retrouve le prix de ce qu'ils ont acheté en connaissance de ce tableau (cf. énoncé).
Code copiable : [Afficher]
 On a une équation matricielle AX = B
On a une équation matricielle AX = B
avec A la matrice des nombres d'objets achetés à chaque fois, X leur prix individuel et B les dépenses totales.
np.linalg.solve(A,B) nous renvoie X, correspondant au vecteur colonne composé de 8,1 et 2.
Un sabre vaut donc 8€, un paquet de chips en vaut 1, et un paquet de craies en vaut 2.
♣ Exercice M8 :
Le tableau de l'énoncé donne la hauteur de pins blancs en fonction de leurs diamètres. Réécrivez ce tableau dans un objet numpy.array et affichez :
- La hauteur moyenne,
- Le diamètre moyen,
- Le diamètre de l’arbre le plus grand.
Code copiable : [Afficher]
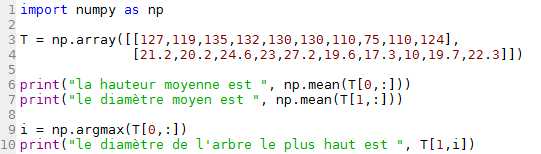
L1. On importe numpy renommé np.
L3. On réécrit le tableau en un array, en gardant la même structure : la première ligne correspond encore à la hauteur et la seconde correspond encore au diamètre.
L6. On affiche à l'aide de la fonction print. La moyenne est faite à l'aide de la fonction mean.
Pour la hauteur moyenne on ne récupère que la première ligne, avec toutes les colonnes : T[0, :]
L7. Pour le diamètre moyen on ne récupère que la seconde ligne, avec toutes les colonnes : T[1, :]
L9. Pour le diamètre de l'arbre le plus haut, on commence par récupérer i qui est l'indice de la colonne où la hauteur est maximale, à l'aide de argmax(T[0, :]) avec T[0, :] car on ne s'intéresse qu'aux valeurs de hauteur.
L10. On affiche le diamètre se situant à l'indice i, donc T[1,i].
Un chevalier et un martien vont au supermarché trois fois dans la semaine. Leurs nourrices voudraient savoir s'ils font attention aux prix.
A l'aide de la fonction np.linalg.solve, retrouve le prix de ce qu'ils ont acheté en connaissance de ce tableau (cf. énoncé).
Code copiable : [Afficher]
import numpy as np
A = np.array([[1,3,2],[2,1,1],[5,2,3]])
B = np.array([[15],[19],[48]])
print(np.linalg.solve(A,B))
A = np.array([[1,3,2],[2,1,1],[5,2,3]])
B = np.array([[15],[19],[48]])
print(np.linalg.solve(A,B))
 On a une équation matricielle AX = B
On a une équation matricielle AX = Bavec A la matrice des nombres d'objets achetés à chaque fois, X leur prix individuel et B les dépenses totales.
np.linalg.solve(A,B) nous renvoie X, correspondant au vecteur colonne composé de 8,1 et 2.
Un sabre vaut donc 8€, un paquet de chips en vaut 1, et un paquet de craies en vaut 2.
♣ Exercice M8 :
Le tableau de l'énoncé donne la hauteur de pins blancs en fonction de leurs diamètres. Réécrivez ce tableau dans un objet numpy.array et affichez :
- La hauteur moyenne,
- Le diamètre moyen,
- Le diamètre de l’arbre le plus grand.
Code copiable : [Afficher]
import numpy as np
T = np.array([[127,119,135,132,130,130,110,75,110,124],
[21.2,20.2,24.6,23,27.2,19.6,17.3,10,19.7,22.3]])
print("la hauteur moyenne est ", np.mean(T[0,:]))
print("le diamètre moyen est ", np.mean(T[1,:]))
i = np.argmax(T[0,:])
print("le diamètre de l'arbre le plus haut est ", T[1,i])
T = np.array([[127,119,135,132,130,130,110,75,110,124],
[21.2,20.2,24.6,23,27.2,19.6,17.3,10,19.7,22.3]])
print("la hauteur moyenne est ", np.mean(T[0,:]))
print("le diamètre moyen est ", np.mean(T[1,:]))
i = np.argmax(T[0,:])
print("le diamètre de l'arbre le plus haut est ", T[1,i])

L1. On importe numpy renommé np.
L3. On réécrit le tableau en un array, en gardant la même structure : la première ligne correspond encore à la hauteur et la seconde correspond encore au diamètre.
L6. On affiche à l'aide de la fonction print. La moyenne est faite à l'aide de la fonction mean.
Pour la hauteur moyenne on ne récupère que la première ligne, avec toutes les colonnes : T[0, :]
L7. Pour le diamètre moyen on ne récupère que la seconde ligne, avec toutes les colonnes : T[1, :]
L9. Pour le diamètre de l'arbre le plus haut, on commence par récupérer i qui est l'indice de la colonne où la hauteur est maximale, à l'aide de argmax(T[0, :]) avec T[0, :] car on ne s'intéresse qu'aux valeurs de hauteur.
L10. On affiche le diamètre se situant à l'indice i, donc T[1,i].